Тоді дана система рівнянь (2.101) має наступний діагональний канонічний вид:
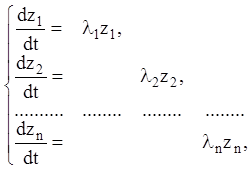 (2. 130)
(2. 130)
де рівність чисел ![]() (кратність характеристичних чисел матриці
P) не виключається.
(кратність характеристичних чисел матриці
P) не виключається.
Висновок: будь-яку
лінійну однорідну систему рівнянь (2.101) можна привести до квазідіагонального
виду (2.127) у випадку, якщо серед елементарних дільників матриці коефіцієнтів ![]() є кратні, або ж до чисто діагонального виду
(2.130) у випадку, коли всі елементарні дільники указаної матриці є простими.
є кратні, або ж до чисто діагонального виду
(2.130) у випадку, коли всі елементарні дільники указаної матриці є простими.
Канонічний вид системи диференціальних рівнянь самого загального виду (2.127) допускає послідовне інтегрування кожної групи рівнянь, починаючи з останнього. А в окремому випадку канонічної системи (2.130) кожне рівняння інтегрується в елементарні (експонентних) функціях незалежно від інших. У цьому й складаються характерні риси канонічних систем й їхньої переваги перед даними (не канонічними) системами виду (2.101), що й обумовлює практичне застосування указаних систем канонічного виду.
З вище викладеного, укажемо алгоритми матричного методу побудови загального розв'язання лінійних однорідних систем з постійними коефіцієнтами (2.101) і розглянемо кілька прикладів розв'язання таких систем. Алгоритм розв'язання:
1) записуємо лінійну систему (2.101) у вигляді матричного рівняння (2.102), де P - транспонована матриця коефіцієнтів системи (2.101);
2) приводимо матрицю P до канонічної жорданової формі й, використовуючи
рівність ![]() , знаходимо матрицю U й
, знаходимо матрицю U й ![]() ;
;
3) знаходимо інтегральну матрицю Z рівняння (2.122), використовуючи формулу (2.123);
4) підставляємо знайдену інтегральну матрицю Z у формулу (2.124), якщо буде потреба в інтегральній матриці Y комплексні розв'язання замінивши відповідними дійсними розв'язаннями;
5) записуємо загальне розв'язання системи, будуя лінійні комбінації
елементів отриманої матриці Y по стовпцях з довільними постійними коефіцієнтами
![]()
Приклад 19. Знайти загальне розв'язання системи 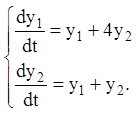
Розв’язання.
1) Записуємо матрицю P, транспонуючи матрицю коефіцієнтів системи 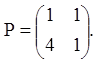
2) Приводимо матрицю P до канонічної жорданової формі. Для цього
записуємо характеристичне рівняння й знаходимо характеристичні числа ![]() тобто
тобто
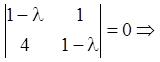
![]()
Простим корінням характеристичного рівняння відповідають прості
елементарні дільники матриці P: ![]() ,
, ![]() . У силу цього, нормальна жорданова форма
матриці A має вигляд:
. У силу цього, нормальна жорданова форма
матриці A має вигляд:
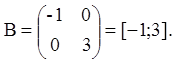
З формули ![]() маємо, що UB = PU або в
розгорнутому виді, поклавши
маємо, що UB = PU або в
розгорнутому виді, поклавши 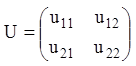 , знаходимо:
, знаходимо:
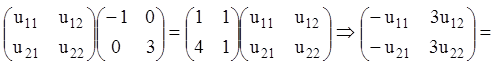
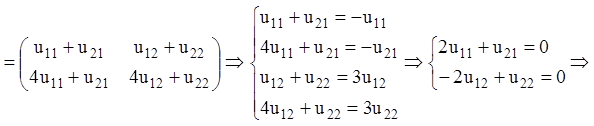
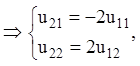
звідки, поклавши, ![]()
![]() знаходимо
знаходимо ![]()
![]()
Тоді матриця:
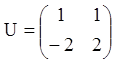
і зворотна матриця:
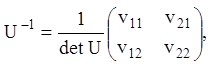
де ![]() –
алгебраїчні доповнення елементів матриці U має вигляд:
–
алгебраїчні доповнення елементів матриці U має вигляд:
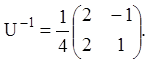
3) З огляду на (2.123) знаходимо інтегральну матрицю:
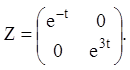
4) Відповідно до формули (2.124) знаходимо інтегральну матрицю даної системи:
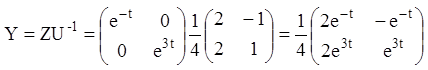
або
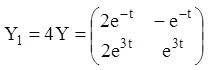
5) Тоді загальне рішення даної системи запишеться у вигляді лінійної комбінації:
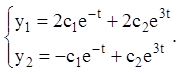
Приклад 20. Знайти загальне розв'язання системи
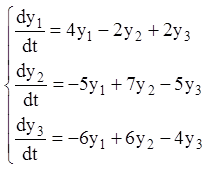
Розв’язання
1) Аналогічно попередньому, одержуємо:
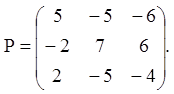
2) 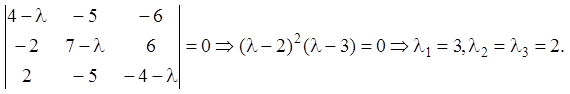
Ранг матриці 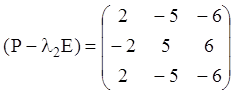 дорівнює
дорівнює ![]() отже,
число елементарних дільників, що відповідають
отже,
число елементарних дільників, що відповідають ![]() дорівнює
дорівнює
![]() . Отже, елементарними дільниками матриці P
будуть
. Отже, елементарними дільниками матриці P
будуть ![]() ,
,![]() ,
, ![]() .
.
Тоді жорданова форма матриці P має вигляд:
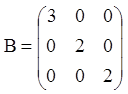 .
.
Знаходимо матрицю U, використовуючи рівність UB = PU, тобто:
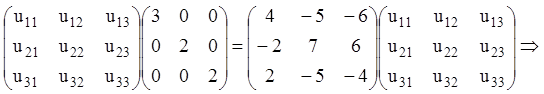
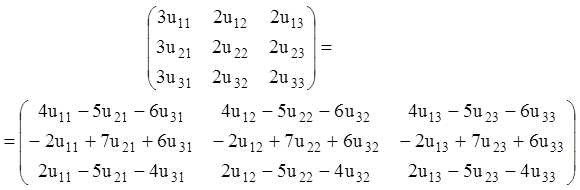
Записана матрична рівність рівносильна наступній системі алгебраїчних рівнянь:
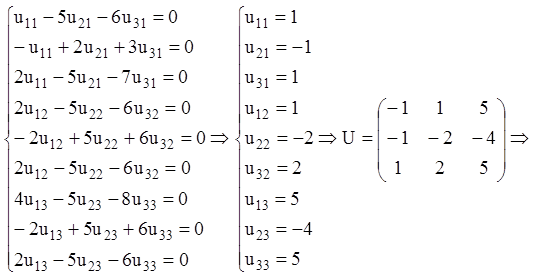
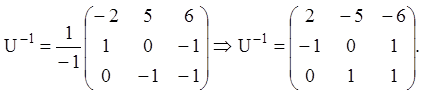
3) З огляду на (2.123), знаходимо 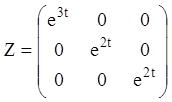
4) 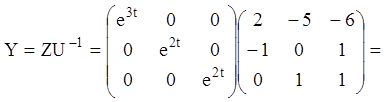
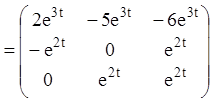 .
.
5) Загальне розв'язання запишеться:
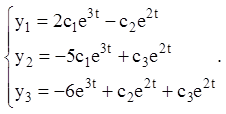
Приклад 21. Розв’язати систему 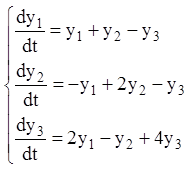 ,
якщо
,
якщо
![]()
Розв’язок.
1) 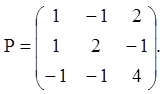
2) 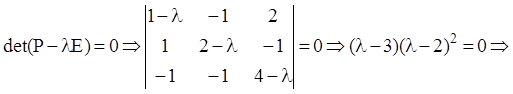
![]() Ранг матриці
Ранг матриці 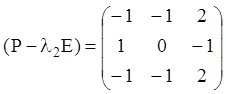 дорівнює
дорівнює ![]() , тому
кількість елементарних дільників, що відповідають цьому характеристичному числу
дорівнює
, тому
кількість елементарних дільників, що відповідають цьому характеристичному числу
дорівнює ![]() , а це значить, що елементарні дільники
мають вигляд
, а це значить, що елементарні дільники
мають вигляд ![]() і жорданова форма матриці P
запишеться:
і жорданова форма матриці P
запишеться:
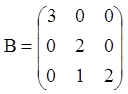 .
.
Знаходимо матрицю U з рівності UB = PU, тобто:
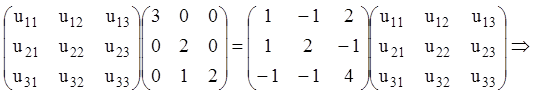
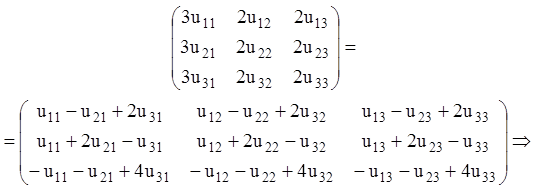

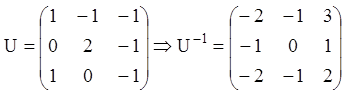
3) Тоді, з огляду на (2.123), (2.114), (2.115), одержуємо:
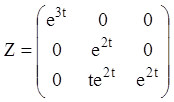
4) 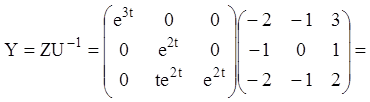
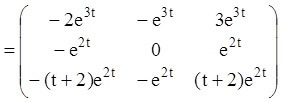
5) Загальне розв'язання запишеться:
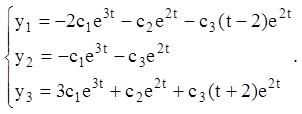
6) Шукаємо частинне розв'язання, використовуючи початкові умови:
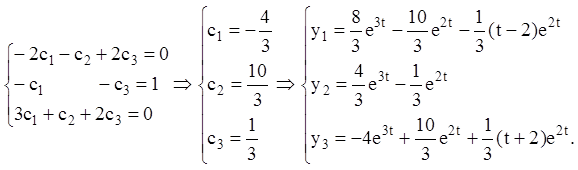
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.