Матричний метод розв'язання однорідних лінійних систем з постійними коефіцієнтами, страница 4

2. Розглянемо загальний випадок, коли матриця P має s < n елементарних дільників різних ступенів, тобто коли не всі елементарні дільники є простими або ж всі вони не є простими. Нехай вони мають вигляд:

                                  (2. 109)

причому серед характеристичних чисел  матриці P можуть бути рівні, а і є цілими позитивними степенями. Згідно (2.41), матриця P перетворенням подоби приводиться до квазідіагонального виду в нормальної жорданової формі:

                               (2. 110)

де   (j = 1,2,…,s) «нижні» жорданові клітки -го порядку виду (2.40). Тепер інтегральна матриця з урахуванням (2.59), (2.57) запишеться:

.                                    (2.111)

Після множення (2.111) ліворуч на матрицю  виду (2.107) одержуємо інтегральну матрицю:

                                       (2. 112)

Обчислимо матрицю як складовий елемент квазідіагональної матриці вираження (2.112). Розглянемо інтерполяційний многочлен для функції , визначений на спектрі матриці J. З огляду на (2.52) він має вигляд:

.

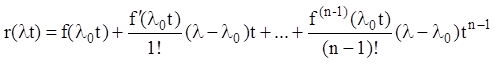Тоді, згідно (2.55) і з урахуванням , знаходимо:

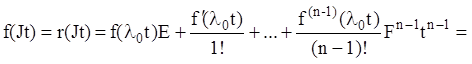
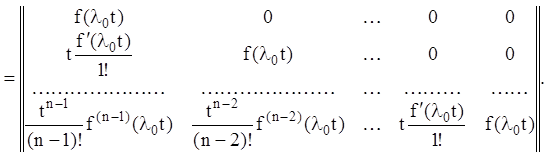                (2.113)

З огляду на вираз (2.113) і поклавши запишемо обчислену матрицю у вигляді:

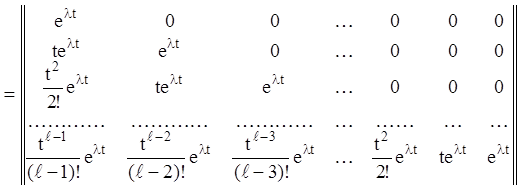.              (2.114)

Зокрема, при буде мати:

Трикутна матриця (2.114) має цікаву особливість щодо коефіцієнтів при в елементах її рядків. Зазначені вище коефіцієнти всіх верхніх рядків можна одержати послідовним диференціюванням коефіцієнтів в елементах останнього рядка.

Розглянемо тепер інтегральну матрицю (2.112) з урахуванням виду (2.114) кліток квазідіагональної матриці й постійної матриці виду (2.107). Очевидно вона буде матрицею n-го порядку, що складає з S груп, що відповідають кліткам квазідіагональної матриці, і утримуючої в кожній групі відповідно  розв'язань. Кожна j-я група (j = 1,2,...,s) має наступну структуру:

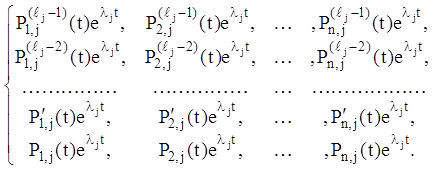                      (2. 115)

У силу відзначеної особливості коефіцієнтів при трикутної матриці (2.114) кожна група рядків інтегральної матриці n-го порядку володіє тим же властивістю щодо коефіцієнтів при своїх елементів. Тому всі розв'язання кожної групи (8.115), що утворять у них  рядків, утворюються із останніх розв'язань у групах послідовним диференціюванням коефіцієнтів при , що мають вид поліномів степенів не вище . Але серед цих коефіцієнтів розв'язань, що перебувають в останніх рядках кожної групи, найдеться, принаймні, один, що має степінь, рівний , де  – степінь елементарного дільника, що відповідає характеристичному числу .

Із установленої структури інтегральної матриці (фундаментальної системи розв'язань), що складає з s груп розв'язань однакової структури, можна одержати вид розв'язань, що відповідають характеристичному числу  різної кратності.

Нехай – характеристичне число кратності  і йому відповідає лише один елементарний дільник що можливо, коли матриця n-го порядку  має ранг Тоді цьому характеристичному числу буде відповідати одна група розв'язань виду (2.115).

Припустимо тепер, що для характеристичного числа  кратності матриця  має ранг де . Тоді числу відповідає k елементарних дільників

                                 (2. 116)

причому . Тоді такому кратному характеристичному числу буде відповідати k груп розв'язань виду (2.115), що містять відповідно  розв'язань ( в (2.115) потрібно замінити на (i = 1,2,…,k))...

Зокрема, якщо , те характеристичному числу  кратності k відповідає k простих елементарних дільників

,

а, отже, і k розв'язань такого ж типу, як й у випадку простого характеристичного числа (з постійними коефіцієнтами при ).

У всіх випадках розглянутих вище, характеристичному числу  кратності  буде відповідати  лінійно незалежних розв'язань, що утворять одну або трохи (не більш ) груп виду (2.115).