Практичне заняття №3
Тема заняття: Метод інтегрувальних комбінацій розв'язання систем.
I. Перевірка виконаного домашнього завдання.
II. Теоретичне опитування:
1. Дайте визначення інтегрувальної комбінації.
2. Що потрібно зробити із системою, щоб одержати інтегрувальну комбінацію?
3. Якими будуть інтегрувальні комбінації у випадку однорідних і неоднорідних нормальних систем?
4. Як нормальну систему записати в симетричній формі?
5. Яка ідея побудови інтегрувальної комбінації у випадку симетричних систем?
6. Як можна використовувати властивість ряду рівних відносин для побудови інтегрувальних комбінацій?
7. Скільки потрібно будувати інтегрувальних комбінацій для одержання розв'язання?
III. Розв'язання задач:
Розв’язати методом інтегрувальних комбінацій наступні системи:
1. 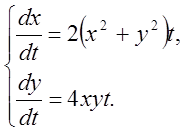
Розв'язання. Складаючи обидва рівняння, одержуємо 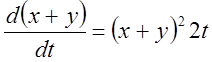 ,
звідки
,
звідки 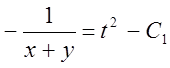 , або
, або 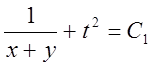 .
.
Віднімаючи обидва
рівняння, одержуємо 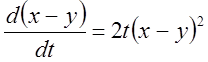 , звідки
, звідки 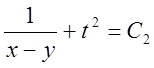 .
.
Отже, знайдені два
перших інтеграли даної системи 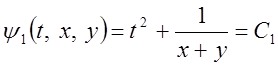 ,
,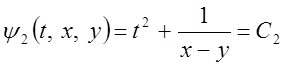 , які є незалежними, тому що якобіан
, які є незалежними, тому що якобіан
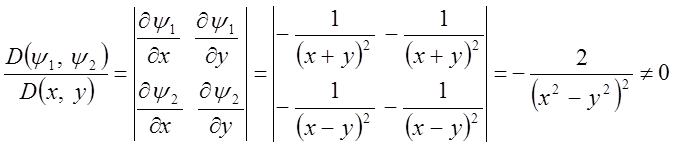 .
.
Загальний інтеграл даної системи 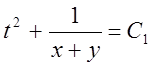 ,
, 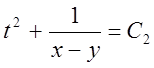 .
Розв'язуючи цю систему щодо невідомих функцій, одержуємо загальне розв'язання
вихідної системи:
.
Розв'язуючи цю систему щодо невідомих функцій, одержуємо загальне розв'язання
вихідної системи:
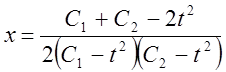 ,
, 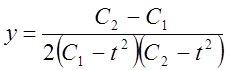 .
.
Відповідь:
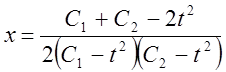 ,
, 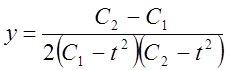 .
.
2. 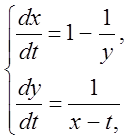
![]() .
.
Розв'язання. Запишемо дану систему у вигляді
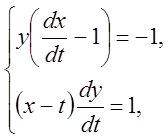 або
або 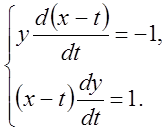
Складаючи останні
рівняння, одержуємо 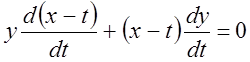 , або
, або 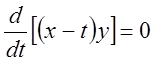 .
Звідси знаходимо перший інтеграл
.
Звідси знаходимо перший інтеграл ![]() . Тому що
. Тому що 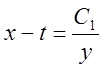 , то друге рівняння системи прийме вид
, то друге рівняння системи прийме вид 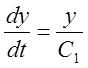 , звідки
, звідки 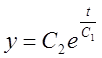 . Отже
. Отже
![]() ,
, 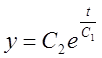 ,
,
звідки одержуємо
загальне розв'язання 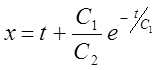 ,
, ![]() .
.
Думаючи
![]() в цих рівностях, знайдемо
в цих рівностях, знайдемо 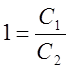 ,
, ![]() , тобто
, тобто ![]() , і шукане частинне розв'язання буде
, і шукане частинне розв'язання буде ![]() ,
, ![]() .
.
Відповідь:
![]() ,
, ![]() .
.
3.
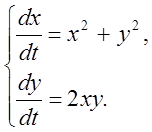 4.
4. 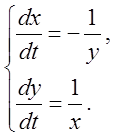 5.
5. 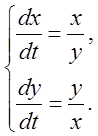 6.
6. 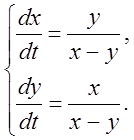 7.
7. 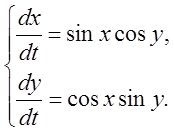
8
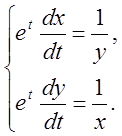 9.
9. 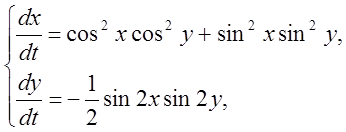
![]() . 10.
. 10. 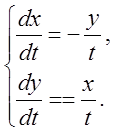
11.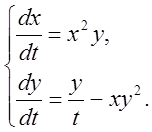 12
12 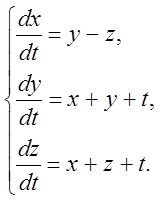 . 13
. 13 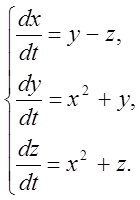 14.
14. 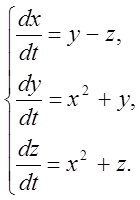
Розв’язати симетричні системи:
1.
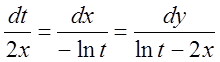 .
.
Розв'язання: Перша інтегрувальна комбінація 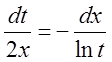 . Розділяючи змінні й інтегруючи, знайдемо
перший інтеграл
. Розділяючи змінні й інтегруючи, знайдемо
перший інтеграл ![]() .
.
Другу
інтегрувальну комбінацію одержимо, використовуючи похідні пропорції. Для цього
складемо чисельники й знаменники дробів даної системи: 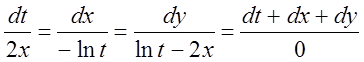 ,
тут
,
тут ![]() ,
, ![]() ,
, ![]() . Звідси
. Звідси ![]() , або
, або ![]() й, виходить,
й, виходить, ![]() .
.
Перші
інтеграли ![]() й
й ![]() дають
загальний інтеграл системи
дають
загальний інтеграл системи ![]() ,
, ![]() , з якого знаходимо загальне розв'язання
системи
, з якого знаходимо загальне розв'язання
системи
![]() ,
, ![]() .
.
Відповідь: ![]() ,
, ![]() .
.
2. 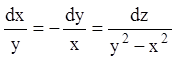 .
.
Розв'язання: Так як 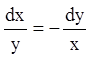 ,
те
,
те ![]() або
або ![]() – перший
інтеграл. Із другого рівняння:
– перший
інтеграл. Із другого рівняння:
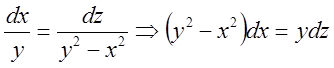 ;
; ![]() .
.
Ділимо на ![]() :
:
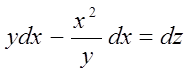
Тому що 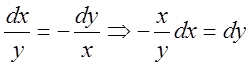 . Тоді
. Тоді 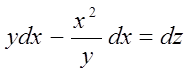 запишеться:
запишеться:
![]() .
.
Перші інтеграли системи: 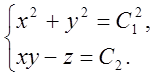
Відповідь: 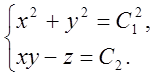
3. 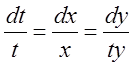 . 4.
. 4. 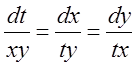 . 5.
. 5. 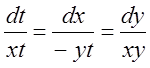 . 6.
. 6. 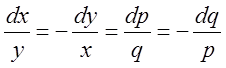 .
.
7. 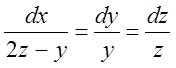 . 8.
. 8. 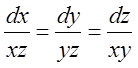 . 9.
. 9. 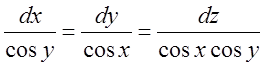 .
.
IV. Домашнє завдання:
1. Підготувати теоретичний матеріал по темі «Загальна теорія лінійних систем».
2. Розв’язати вдома задачі, що залишилися
3. Принести виконану частину індивідуального завдання по заданій темі.
4. Підготується до самостійній роботі із пройденого матеріалу на 45 хвилин.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.