Проведення самостійної роботи. Загальна теорія лінійних систем: Практичне заняття № 4

Практичне заняття №4

Тема заняття: Проведення самостійної роботи. Загальна теорія лінійних систем.

I. Перевірка виконаного домашнього завдання.

II. Теоретичне опитування:

1. Яка система диференціальних рівнянь називається лінійної?

2. Який вид має векторна форма запису неоднорідної й однорідної систем, і що означають, вектор і матриця, що там стоять?

3. Як уводиться лінійний оператор ?

4. Перелічите лінійні властивості лінійного оператора .

5. Теореми 1,2,3, про розв'язання лінійної однорідної системи.

6. Визначення лінійно залежної й лінійно незалежної системи векторів на . Визначник Вронського.

7. Теорема про визначник Вронського розв'язань  ОЛС .

8. Дати визначення фундаментальній системі розв'язань й інтегральної матриці системи.

9. Теорема про існування фундаментальної системи розв'язань ЛОС  із неперервними на  коефіцієнтами .

10. Теорема об визначнику Вронського  лінійно незалежних розв'язань  ЛОС.

11. Теорема про вид загального розв'язання ЛОС.

12. Теорема про вид загального розв'язання ЛНС.

13. Який вид має формула Остраградського-Лиувиля?

14. Принцип суперпозиції розв'язань.

III. Розв'язання задач:

Чи утворять векторів-функції фундаментальну систему розв'язань ЛОС?

1. 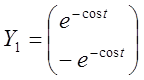, 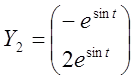. 2. , .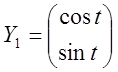

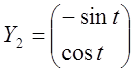Установити лінійну залежність або незалежність систем векторів.

1. 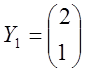, 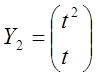. 2.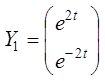  

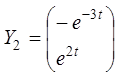
IV. Домашнє завдання:

1. Підготувати теоретичний матеріал по темі «Матричний метод розв'язання лінійних однорідних систем з постійними коефіцієнтами».

2. Розв’язати вдома задачі, що залишилися

3. Принести виконану частину індивідуального завдання по заданій темі.