Нехай дана лінійна неоднорідна система рівнянь із постійними коефіцієнтами:
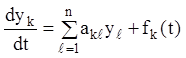 (k =
1,2,…,n) (2...147)
(k =
1,2,…,n) (2...147)
або рівносильне їй векторно-матричне рівняння:
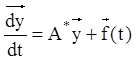 (2. 148)
(2. 148)
с квадратною матрицею
коефіцієнтів ![]() й n-мірних векторів
й n-мірних векторів
![]()
У п. 2.4, 2.5 дійсної глави розглянуте питання приведення до канонічного виду лінійної однорідної системи (2.101) або ж векторно-матричного рівняння:
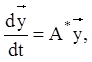 (2. 149)
(2. 149)
яке утворюється із (2.148)
при ![]() Таке ж ствердження має місце й для
лінійного неоднорідного векторно-матричного рівняння (2.148);
Таке ж ствердження має місце й для
лінійного неоднорідного векторно-матричного рівняння (2.148);
Теорема. Нехай
дане лінійне неоднорідне векторно-матричне рівняння (2.148), де ![]() й
й ![]() –
n-мірні вектори, а
–
n-мірні вектори, а ![]() – постійна матриця n-го порядку.
Завжди існує лінійне не вироджене перетворення
– постійна матриця n-го порядку.
Завжди існує лінійне не вироджене перетворення
![]() або
або ![]() (2.150)
(2.150)
де ![]() –
невироджена постійна матриця, обумовлена перетворенням подоби
–
невироджена постійна матриця, обумовлена перетворенням подоби
![]() (2. 151)
(2. 151)
яке приводить рівняння (2.148) до векторно-матричного рівняння канонічного виду
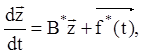
де матриця ![]() – подібна матриця жорданової форми до
матриці
– подібна матриця жорданової форми до
матриці ![]() з матрицею подоби
з матрицею подоби ![]() ,
а вектор
,
а вектор ![]() .
.
Отже, лінійну неоднорідну систему рівнянь із постійними коефіцієнтами
(2.147), також як і відповідну лінійну однорідну систему рівнянь, завжди можна
привести до канонічного виду, причому перетворення ![]() ,
матриці
,
матриці ![]() й
й ![]() у них
однакові.
у них
однакові.
Дійсно, з лінійного перетворення (2.150) рівняння (2.148) і перетворення подоби (2.151) треба, що:
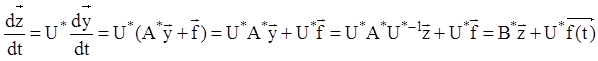
або, з урахуванням позначення
![]() одержуємо:
одержуємо:
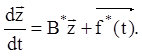
Відомо, що загальне розв'язання неоднорідної лінійної системи ![]() дорівнює сумі загального розв'язання
відповідної однорідної системи
дорівнює сумі загального розв'язання
відповідної однорідної системи ![]() й частинного розв'язання
неоднорідної системи
й частинного розв'язання
неоднорідної системи ![]()
Оскільки для відповідних однорідних лінійних систем з постійними коефіцієнтами можна ефективно побудувати загальне розв'язання, то фундаментальні системи розв'язань стають відомими, а це дає можливість застосувати метод варіації довільних постійних до лінійних неоднорідних систем й одержати загальне розв'язання у квадратурах.
Розглянемо лінійні неоднорідні систем з постійними коефіцієнтами, зупинимося на прикладах застосування методу Лагранжа.
Приклад 26. Проінтегрувати неоднорідну систему рівнянь:
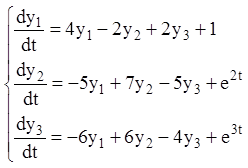
Розв’язання. Загальне розв'язання відповідної однорідної системи рівнянь має вигляд:
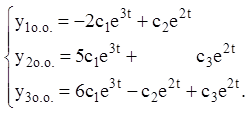
Шукаємо частинне розв'язання неоднорідної системи у вигляді:
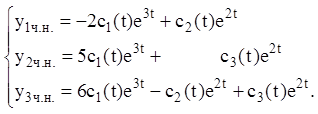 (2.
152)
(2.
152)
У нашому випадку
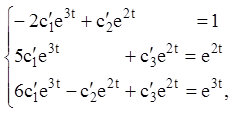
Звідки:
![]()
Отже:
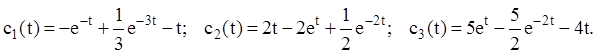
Підставляючи ці значення в систему (2.152), одержимо частинне розв'язання неоднорідної системи:
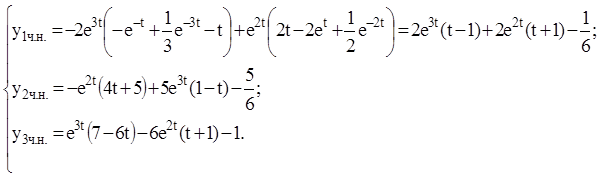
Тоді загальне розв'язання неоднорідної системи запишеться:
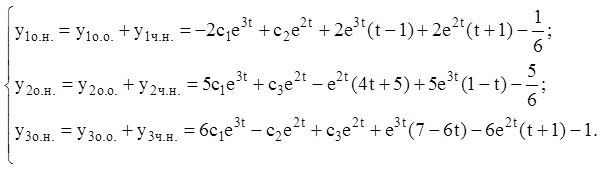
Розглянемо лінійну неоднорідну систему (2.147), у якій функції
![]() (k =
1,2,…,n) (2...153)
(k =
1,2,…,n) (2...153)
де ![]() –
многочлен степеня
–
многочлен степеня ![]() можуть бути дійсними або комплексними.
можуть бути дійсними або комплексними.
Відповідно до сформульованої теореми, розглянуту неоднорідну систему можна привести до канонічного виду, що складає з s груп рівнянь, де s - число всіх елементарних дільників матриці коефіцієнтів системи (2.127). Кожна з s груп рівнянь допускає послідовне інтегрування, починаючи з останнього рівняння.
а) якщо ![]() й
й ![]() , те
частинне розв'язання даної неоднорідної системи (2.153) має вигляд:
, те
частинне розв'язання даної неоднорідної системи (2.153) має вигляд:
![]() (i =
1,2,…,n), (2...154)
(i =
1,2,…,n), (2...154)
де ![]() –
многочлен степеня g.
–
многочлен степеня g.
При практичному знаходженні частинних розв'язань виду (2.154) можна
використати метод невизначених коефіцієнтів. При цьому частинне розв'язання
записується у вигляді (2.154), де ![]() – багаточлен з
невизначеними коефіцієнтами ступеня g. Ці невідомі коефіцієнти рішення можна знайти
підстановкою розв'язання у вихідну систему й прирівнюванням коефіцієнтів при
однакових степенях t у лівих і правих частинах отриманих рівностей після
скорочення на
– багаточлен з
невизначеними коефіцієнтами ступеня g. Ці невідомі коефіцієнти рішення можна знайти
підстановкою розв'язання у вихідну систему й прирівнюванням коефіцієнтів при
однакових степенях t у лівих і правих частинах отриманих рівностей після
скорочення на ![]() .
.
б) Якщо
![]() і
і ![]() (2.155)
(2.155)
то частинне розв'язання шукаємо у вигляді:
![]() (2. 156)
(2. 156)
де ![]() й
й
![]() – многочлени з невизначеними коефіцієнтами
степеня g, де g –
більший степінь многочленів
– многочлени з невизначеними коефіцієнтами
степеня g, де g –
більший степінь многочленів ![]() й
й ![]() , що входять у неоднорідність (2.155).
Невідомі коефіцієнти поліномів
, що входять у неоднорідність (2.155).
Невідомі коефіцієнти поліномів ![]() і
і ![]() знаходяться методом невизначених
коефіцієнтів, тобто підстановкою розв'язання в систему й порівнянням
коефіцієнтів при подібних членах
знаходяться методом невизначених
коефіцієнтів, тобто підстановкою розв'язання в систему й порівнянням
коефіцієнтів при подібних членах ![]() й
й ![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.