Методи інтегрування лінійних неоднорідних систем з постійними коефіцієнтами, страница 2

в) Якщо й має вигляд (2.153), те інтегруючи канонічну систему одержують розв'язання виду

 (i = 1,2,…,n)                                            (2...157)

де – многочлени степеня не вище (g + p), g – найбільший степінь многочлена, що входить у неоднорідність (2.153), а p – найвищий степінь елементарного дільника виду , що відповідають характеристичному числу  В цьому випадку частинне розв'язання шукаємо у вигляді:

                                                     (2. 158)

де – многочлени з невизначеними коефіцієнтами ступеня (g + p), коефіцієнти яких шукаються як й у випадку a), але розв'язання побудованих систем неоднозначно.

г) Якщо й  має вигляд (2.156), то частинне розв'язання шукається у вигляді:

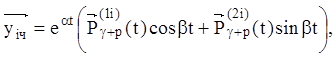                               (2. 159)

,

де  – многочлени з невизначеними коефіцієнтами степеня не перевищуючого (g + p), де g – найбільший степінь многочленів, що входять в (2.156), p – найвищий степінь елементарного дільника виду відповідному характеристичному числу Як і раніше невідомі коефіцієнти поліномів  і   визначаються шляхом порівняння коефіцієнтів при подібних членах  й у рівняннях вихідної системи після підстановки в них побудованого розв'язання (2.159). При цьому розв'язання побудованих систем неоднозначно.

Приклад 27.Проінтегрувати неоднорідну систему:

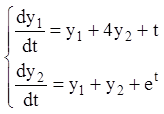
Розв’язання. Корінь характеристичного многочлена матриці коефіцієнтів системи Загальне розв'язання ЛОС має вигляд:

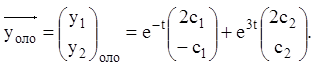
Праву частину ЛНС запишемо у вигляді , тобто:

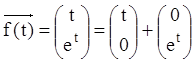
і, використовуючи принцип суперпозиції, запишемо вид частинного розв'язання

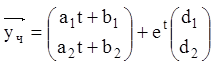 тобто

Підставляючи в ЛНС із правою частиною

,

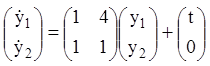одержуємо:

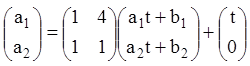 або

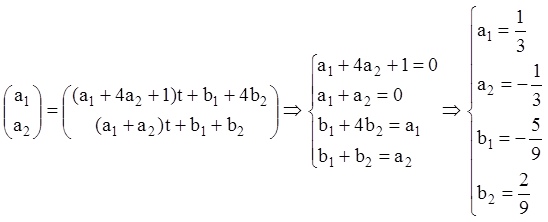
Тепер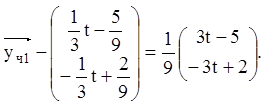

Аналогічно підставляємо  в ЛНС із правою частиною :

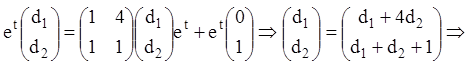
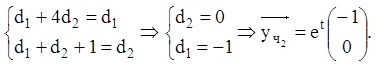
Тоді .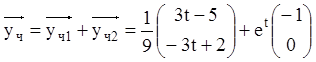

Загальне розв'язання ЛНС дорівнює:

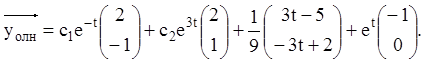
Приклад 28.Розв’язати систему:

якщо характеристичне рівняння відповідної однорідної системи має корені і загальне розв'язання системи має вигляд

Розв’язання. З огляду на, що корінь характеристичного рівняння дійсний і різні (випадок а)),

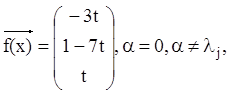
частинне розв'язання неоднорідної системи шукаємо у вигляді:

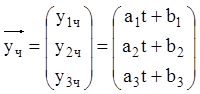
Підставляємо в ЛНС, представивши її у векторній формі,

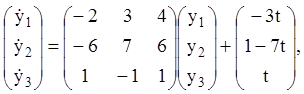
одержуємо

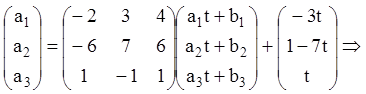
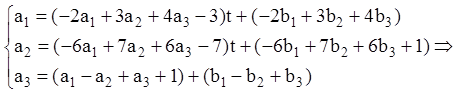
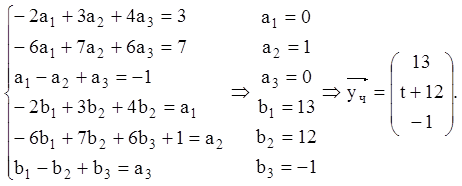
Тоді загальне розв'язання ЛНС у векторній формі запишеться:

3. Побудова інтегрувальних комбінацій (метод Даламбера)

Як було зазначено вище, лінійні системи можна інтегрувати й загальними методами, у тому числі методом інтегрувальних комбінацій. При цьому для побудови інтегрувальних комбінацій у випадку системи лінійних рівнянь із постійними коефіцієнтами існує загальний метод, запропонований Даламбером. Розглянемо цей метод у випадку лінійної системи двох рівнянь:

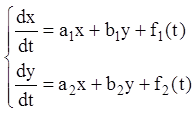                                                     (2. 160)

Перепишемо останнє рівняння у вигляді:

                                     (2. 161)

Виберемо число  так, щоб

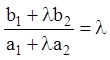
і в такий спосіб одержимо квадратне рівняння :

                                              (2. 162)

Тоді (2.161) приводиться до рівняння, лінійному відносно

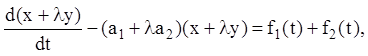
інтегруючи яке, одержуємо:

                             (2. 163)

або:

Можливі наступні випадки:

1) корені квадратного рівняння (2.162) дійсні й різні. Тоді маємо два інтеграли системи:

2) корені квадратного рівняння (2.162) комплексні . Дорівнюючи дійсних і мнимих складових обох частин рівняння

також одержимо два інтеграли. Тут й – довільні постійні.

3) корені квадратного рівняння (2.162) кратні В цьому випадку одержуємо тільки один інтеграл, що дозволяє звести питання до інтегрування одного лінійного рівняння з однією невідомою функцією.

Приклад 29. Проінтегрувати методом Даламбера систему:

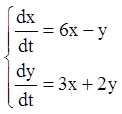
Розв’язання. Помножимо друге рівняння на ( і додадим з першим:

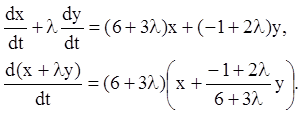
Інтегрувальна комбінація може бути отримана, якщо:

            

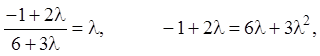
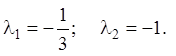
У першому випадку для 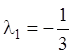, одержуємо:

        

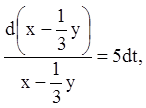
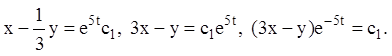
У другому випадку  одержуємо:

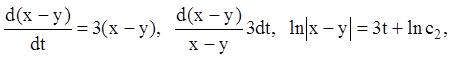
Тоді загальний інтеграл системи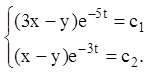

Зауваження. Методом Даламбера можна розв’язувати й канонічні системи (системи, які розв’зуються щодо старших похідних, праві частини яких є лінійними функціями з постійними коефіцієнтами).

Розглянемо систему двох рівнянь n-го порядку з постійними коефіцієнтами:

Помножимо друге рівняння на ( і складемо з першим рівнянням, одержимо:

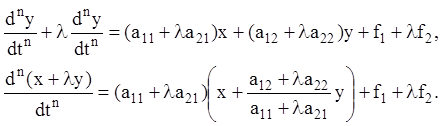
Якщо l вибрати з умови 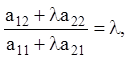то одержимо рівняння n-го порядку з постійними коефіцієнтами U = x + ly:

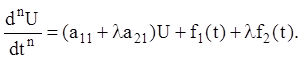
Якщо знайдено загальне розв'язання останнього рівняння то, якщо корені квадратного рівняння різні, маємо систему:

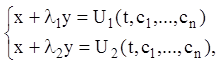
з якої можна знайти загальне розв'язання даної системи