Метод Ейлера розв'язання лінійних однорідних систем з постійними коефіцієнтами

2.5 Метод Ейлера розв'язання лінійних однорідних систем з постійними коефіцієнтами

Нехай дана система лінійних однорідних диференціальних рівнянь із постійними коефіцієнтами:

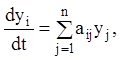 (j = 1,2,…,n)                                          (2...131)

де . Уводячи позначення:

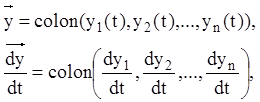                         (2. 132)

запишемо систему у векторному виді

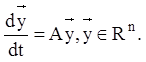                                                       (2. 133)

Розв'язанням ЛОС (2.133) є деякий диференційований вектор

,                                              (2.134)

який задовольняє рівнянню (2.133) на a < t < b. Якщо побудувати n лінійно незалежних розв'язань рівняння (2.133), то загальне розв'язання запишеться у вигляді:

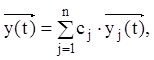                                                          (2. 135)

де – довільні постійні.

Розв'язання системи (2.133) будемо шукати у вигляді Ейлера:

                                                              (2. 136)

у якому координати n-мірного вектора й числа l підлягають визначенню. Підставляючи (2.136) в (2.133), одержуємо:

Скорочуючи на , одержуємо

                                                                (2. 137)

або:

або:

                                                           (2. 138)

де E - одинична матриця n-го порядку.

Рівність (2.137) показує, що вектор  за допомогою матриці A перетвориться в паралельний йому вектор , а це значить, що вектор є власним вектором матриці A, що відповідає власному значенню l. У скалярній формі рівність (2.138) являє собою лінійну однорідну систему алгебраїчних рівнянь. У силу того, що , число l повинне визначаться з характеристичного рівняння (нас цікавить ненульове розв'язання системи (2.138)):

                                                         (2. 139)

Розглянемо різні випадки характеристичних корінь рівняння (2.139).

1. Корені дійсні й різні.

Тоді матриця A має n лінійно незалежних власних векторів  відповідним власним числам , система розв'язань:

                                                    (2. 140)

лінійно незалежна і є фундаментальною системою розв'язань ЛОС (2.133). Тоді, з урахуванням (2.135), одержуємо загальне розв'язання:

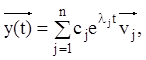
  .                                             (2.141)

2. Корені дійсні й кратні.

У попередньому параграфі встановлені види відповідних частин загального розв'язання для характеристичних чисел різних видів і кратностей. Це дає можливість сформулювати наступну теорему:

Нехай – характеристичні числа постійної матриці A коефіцієнтів ЛОС (2.133),  відповідно їхній кратності в мінімальному многочлені y(l) матриці A. Тоді будь-яка фундаментальна матриця системи може бути записана у вигляді:

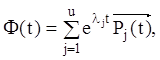                                                  (2. 142)

де – n-мірні вектори-стовпці з поліноміальними елементами степеня не вище , причому степінь хоча б одного елемента вектора  дорівнює .

Практично шукані частини загального розв'язання з невизначеними коефіцієнтами підставляються у вихідну систему рівнянь, провадиться скорочення на , а потім прирівнюються коефіцієнти при однакових степенях t лівих і правих частин отриманих рівностей. У результаті одержуємо систему лінійних алгебраїчних рівнянь щодо невідомих коефіцієнтів рішень виду (2.142), з яких всі вони визначаються через  коефіцієнтів, що залишаються довільними.

Тоді загальне розв'язання системи рівнянь приймає вид:

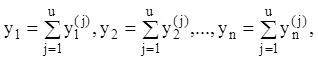                                   (2. 143)

тобто є сумою всіх відповідних частин загального розв'язання для різних характеристичних чисел  (j = 1,2,…,u)...

3. Корені комплексно-сполучені.

У силу спряженості комплексних характеристичних чисел кратності й речовинності матриці A, що відповідають частини загального розв'язання (2.142) будуть також комплексно-сполученими, тобто

  (k = 1,2,…n)..         . (2.144)

Тут  й – поліноми степеня не вище чим , коефіцієнти яких при однакових  k  (k = 1,2,…n) комплексно-сполучені й всі вони в сукупності виражаються через  довільних постійних, використовуючи метод невизначених коефіцієнтів. Однак практично зручніше знаходити ці розв'язання для комплексно-сполучених характеристичних чисел у дійсній формі, використовуючи те, що дійсна й мнима частини комплексного розв'язання є також розв'язаннями вихідної системи рівнянь. Тому, виділяючи з кожного із двох комплексно значних розв'язань (2.144) дійсну й мниму частини, одержимо два шуканих розв'язання в дійсній формі:

  (k = 1,2,…,n),        (2...145)

складових відповідні частини загального розв'язання. При цьому поліноми  й  степені не вище , а їхні дійсні коефіцієнти будуть виражатися через довільних постійних. Підсумовуючи розв'язання (2.145), одержуємо розв'язання: