![]() (k = 1,2,…,n), (2...146)
(k = 1,2,…,n), (2...146)
яке й становить відповідну
частину загального розв'язання для пари комплексно-сполучених характеристичних
чисел ![]() кратності
кратності ![]() .
.
У випадку простих комплексно-сполучених характеристичних чисел поліноми
![]() й
й ![]() вироджуються
в постійні коефіцієнти, які виражаються через дві довільні постійні.
вироджуються
в постійні коефіцієнти, які виражаються через дві довільні постійні.
Практично побудовані з невизначеними коефіцієнтами шукані частини
загального розв'язання, що відповідають парі комплексно-сполучених
характеристичних чисел підставляють у вихідну систему рівнянь, скорочують на ![]() , а потім дорівнюють коефіцієнти при
, а потім дорівнюють коефіцієнти при ![]() й
й ![]()
![]() лівих і правих частин отриманих рівностей.
У результаті одержуємо щодо невідомих коефіцієнтів розв'язань виду (2.146)
систему рівнянь із якої всі вони визначаються через
лівих і правих частин отриманих рівностей.
У результаті одержуємо щодо невідомих коефіцієнтів розв'язань виду (2.146)
систему рівнянь із якої всі вони визначаються через ![]() коефіцієнтів,
що залишаються довільними.
коефіцієнтів,
що залишаються довільними.
Проілюструємо метод Ейлера розглядом ряду конкретних прикладів.
Приклад 22. Розв’язати систему рівнянь 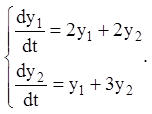
Розв’язання. Становимо характеристичне рівняння й знаходимо його корінь
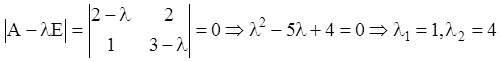 – корені дійсні й
різні, і їм відповідають два лінійно незалежних власних вектори
– корені дійсні й
різні, і їм відповідають два лінійно незалежних власних вектори ![]() й
й ![]() координати
яких ми й знайдемо. Для цього складаємо відповідні системи (2.138).
координати
яких ми й знайдемо. Для цього складаємо відповідні системи (2.138).
Для ![]()
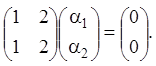
Думаючи ![]() знаходимо
знаходимо ![]() й
вектор
й
вектор ![]() Тоді розв'язання, що відповідає
характеристичному числу
Тоді розв'язання, що відповідає
характеристичному числу ![]() , запишеться:
, запишеться:
![]()
Аналогічно для ![]()
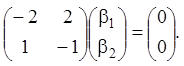
Думаючи ![]() , знаходимо
, знаходимо ![]() й
й ![]() Розв'язання,
що відповідає
Розв'язання,
що відповідає ![]() , має вигляд:
, має вигляд:
![]()
Тоді загальне розв'язання запишеться:
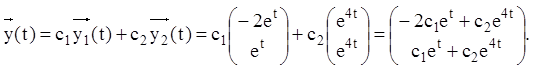
Тому що шуканий вектор ![]() то загальне розв'язання
запишеться:
то загальне розв'язання
запишеться:
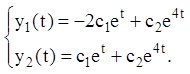
Приклад 23. Розв’язати систему ![]() якщо:
якщо:
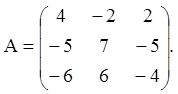
Розв’язання. Знаходимо характеристичні числа матриці A:
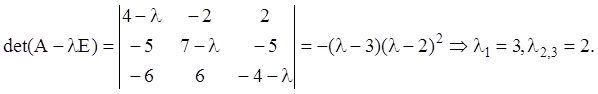
Найбільший загальний дільник всіх мінорів 2-го порядку ![]() тоді мінімальний многочлен матриці A має
вигляд (2.46):
тоді мінімальний многочлен матриці A має
вигляд (2.46):
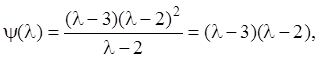
тому загальне розв'язання ЛОС має вигляд:
![]()
Тому що кожне з доданків останньої суми є розв'язанням ЛОС, то,
підставляючи перший доданок, одержуємо систему (2.138) для ![]()
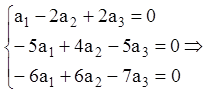
Одним з розв'язань цієї системи буде ![]() а
фундаментальна система розв'язань має вигляд:
а
фундаментальна система розв'язань має вигляд: ![]() де
де ![]()
Аналогічно для другого кореня ![]() (Ще раз
підкреслюємо, що для другого характеристичного числа степінь многочлена
(Ще раз
підкреслюємо, що для другого характеристичного числа степінь многочлена ![]() теж буде нульова, тому що
теж буде нульова, тому що ![]() Тут m2 – кратність
характеристичного числа
Тут m2 – кратність
характеристичного числа ![]() в мінімальному
многочлені):
в мінімальному
многочлені):
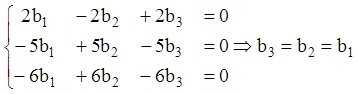 ,
, ![]() і
і ![]() .
.
Думаючи ![]() де
де ![]() й
й ![]() – довільні постійні, одержуємо:
– довільні постійні, одержуємо:
![]()
Таким чином, згідно (2.142), одержуємо розв'язання системи:
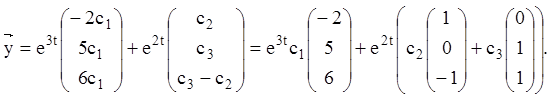
Зверніть увагу на те, що система функцій:
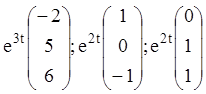
є фундаментальною системою розв'язань ЛОС. Загальне розв'язання:
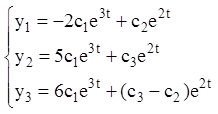
Приклад 24. Розв’язати систему ![]()
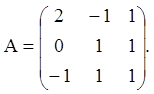
Розв’язання. Складаємо характеристичний многочлен і знаходимо його корінь:
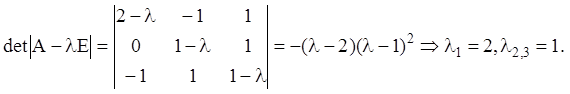
Мінімальний многочлен матриці A має вигляд ![]() , тобто
збігається з характеристичним многочленом. Тому
, тобто
збігається з характеристичним многочленом. Тому ![]() й
й ![]() що означає, що для
що означає, що для ![]() координати
вектора-стовпця
координати
вектора-стовпця ![]() є многочленами нульового степеня
(невизначеними постійними), а для характеристичного числа
є многочленами нульового степеня
(невизначеними постійними), а для характеристичного числа ![]() координати вектора-стовпця
координати вектора-стовпця ![]() є многочленами першого степеня. Таким
чином, загальне розв'язання у векторному виді має вигляд:
є многочленами першого степеня. Таким
чином, загальне розв'язання у векторному виді має вигляд:
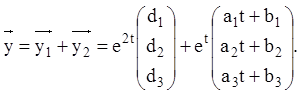
Підставляючи ![]() у дану систему, одержуємо систему
(2.138) для знаходження координат вектора
у дану систему, одержуємо систему
(2.138) для знаходження координат вектора ![]()
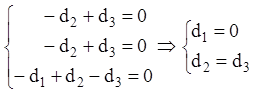 .
.
Тому що характеристичне число ![]() кратності
1, то в розв'язуваній системі одна довільна постійна. Думаючи
кратності
1, то в розв'язуваній системі одна довільна постійна. Думаючи ![]() , одержуємо
, одержуємо ![]() й
й ![]() й
й ![]()
Для знаходження ![]() (i = 1,2,3) підставляємо
(i = 1,2,3) підставляємо
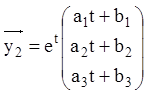 у дану систему, обчисливши попередньо
у дану систему, обчисливши попередньо ![]() . Одержуємо:
. Одержуємо:
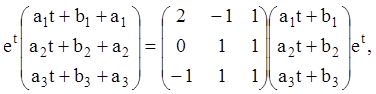
звідки, скорочуючи на ![]() й перемножуючи матриці в правій частині,
одержуємо систему:
й перемножуючи матриці в правій частині,
одержуємо систему:
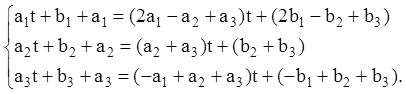
Дорівнюючи коефіцієнти при однакових степенях t, одержуємо:
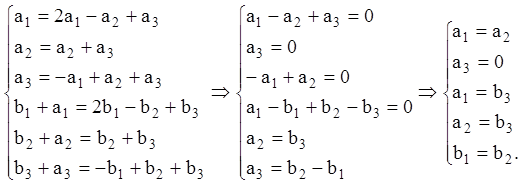
Тому що друге характеристичне число ![]() є
двократним коренем характеристичного многочлена, те розв'язувана система має
дві довільні постійні. Нехай такими будуть
є
двократним коренем характеристичного многочлена, те розв'язувана система має
дві довільні постійні. Нехай такими будуть ![]() й
й ![]() і
і ![]()
![]() Тоді
Тоді ![]()
Тоді ![]() запишеться
запишеться
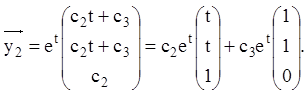
Таким чином, загальне розв'язання ЛОС має вигляд ![]() й
й
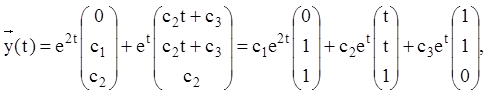
де ![]() –
довільні постійні. При цьому векторів-функції
–
довільні постійні. При цьому векторів-функції
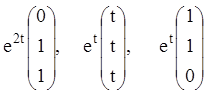
утворять фундаментальну систему розв'язань вихідної ЛОС.
Приклад 25. Розв’язати систему ![]()
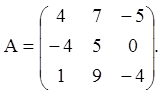
Розв’язання. Складаємо характеристичний многочлен і знаходимо його корінь:
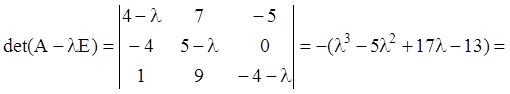
![]()
Характеристичні числа різні, але серед них є комплексно-сполучені.
Знайдемо власний вектор і напишемо розв'язання, що відповідає першому власному числу, використовуючи рівняння (2.138):
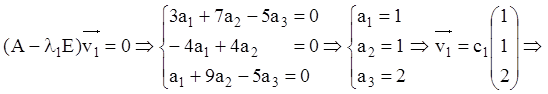
![]()
Знайдемо власний вектор і напишемо розв'язання, що відповідають
власному числу ![]() . Використовуючи (2.138),
одержуємо:
. Використовуючи (2.138),
одержуємо:
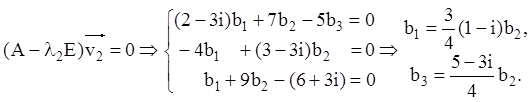
Думаючи ![]() , одержуємо один власний вектор:
, одержуємо один власний вектор:
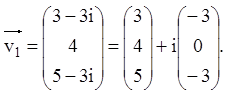
Записуємо розв'язання системи, що відповідає цьому характеристичному числу:
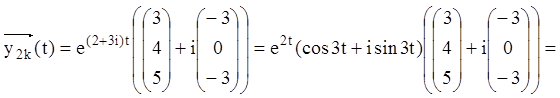
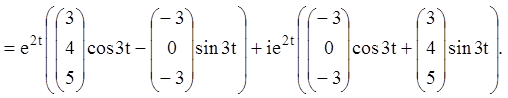
Тому що дійсна й мнима частина комплексного розв'язання ![]() окремо будуть розв'язаннями ЛОС, то
одержуємо два лінійно-незалежних дійсних розв'язання
окремо будуть розв'язаннями ЛОС, то
одержуємо два лінійно-незалежних дійсних розв'язання
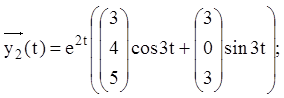
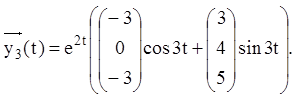
Тому що ![]() – лінійно незалежні розв'язання,
тому загальне розв'язання ЛОС запишеться:
– лінійно незалежні розв'язання,
тому загальне розв'язання ЛОС запишеться:
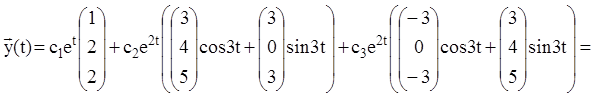
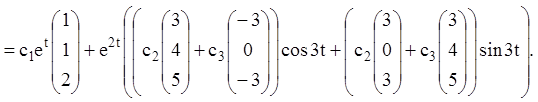
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.