Матричная игра двух игроков: Практическое занятие № 1

Практическое занятие № 1

«Матричная игра двух игроков»

Пример 1

Дана платежная матрица 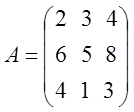. Найти седловую точку игры.

Решение

1-й игрок:

1)  выбираем максимальные элементы по столбцам

2)  выбираем минимальный элемент из выбранных ;

2-й игрок:

1)  выбираем минимальные элементы по строкам

2)  выбираем максимальный элемент из выбранных

 — седловая точка в чистых стратегиях.

Пример 2

Дана платёжная матрица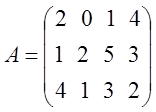. Если встречаются доминируемые стратегии, отбросить их.

Решение

Если для -ой и -ой стратегий I игрока выполняются соотношения  и  по крайней мере для одного , то говорят, что -ая стратегия доминирует (превосходит) -ую стратегию.

Если для -ой и -ой стратегий II игрока выполняются соотношения  и  по крайней мере для одного , то говорят, что -ая стратегия доминирует -ую стратегию.

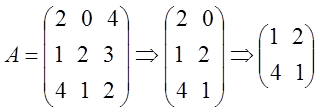
Определим  и :  ;   ; седловой точки в чистых стратегиях нет.

Пример 3

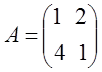
Найти оптимальную смешанную стратегию.

Решение

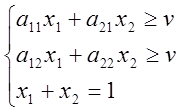1.            2. 

                     

                          

               

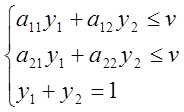
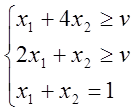
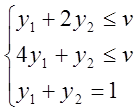
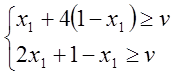
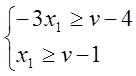
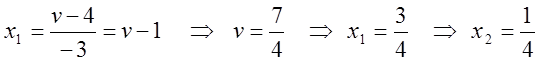
Аналогично .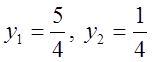

Задание для самостоятельного решения:

Найти оптимальную стратегию в смешанной игре, предварительно исключив доминируемые стратегии:

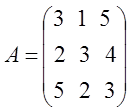
Практическое занятие №2

«Матричные игры двух игроков с матричной суммой»

Пример 1

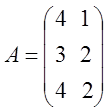
Решение

 — седловая точка

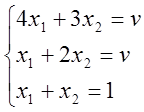
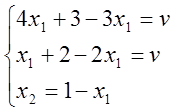
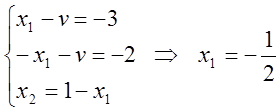                 — невозможно: когда игра имеет седловую точку в чистых стратегиях, то решение получается в отрицательных числах.

Пример 2

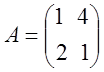
Найти оптимальную стратегию.

Решение

     

1.   

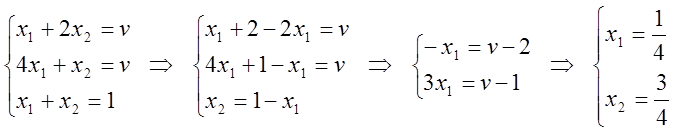
2.

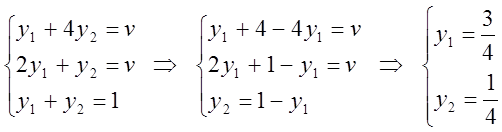
Задание для самостоятельной работы:

Решить матричную игру с нулевой суммой размерности :

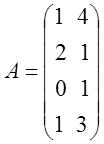
Практическое задание № 3.

«Методы решения матричных игр: решение матричной игры с помощью алгоритма двойственного симплекс метода».

Пример 1

Разберём применение линейного программирования в общем виде:

предположим, что цена игры положительна (u > 0). Если это не так, то всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. Пусть дана матричная игра с матрицей А порядка mхn.

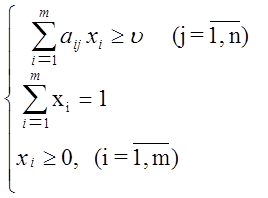
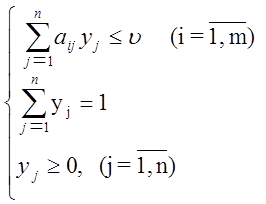
Разделим все уравнения и неравенства в  на u (u > 0) и введём обозначения :

     ,          ,

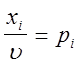
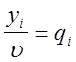
Тогда:

,     ,     ,     ,

,     ,     ,     .

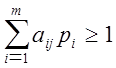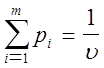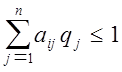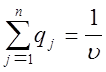Поскольку первый игрок стремится найти такие значения х_i и, следовательно, p_i , чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений  p_i  , при которых

,   .

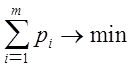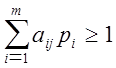Поскольку второй игрок стремится найти такие значения y_j и, следовательно, q_j, чтобы цена игры uбыла наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений  q_j,  , при которых

,   .

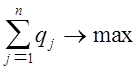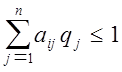Решив эти задачи, получим значения  p_i ,  q_j  и u.Тогда смешанные стратегии:

Пример 2

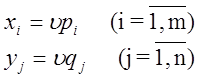
 Найти решение игры, определяемой матрицей.

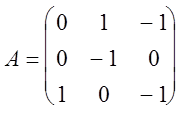
Решение.

При решении этой игры к каждому элементу матрицы А прибавим 1 и получим следующую матрицу

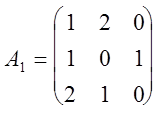
Составим теперь пару взаимно-двойственных задач :

                   

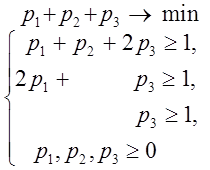
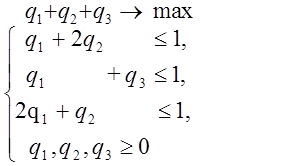
Решим вторую из них

ББ.п.	Q1	q2	q3	q4	q5	q6	Решение	å	Отношение
	-1	-1	-1	0	0	0	0	-3
q4	1	2	0	1	0	0	1	5	—
q5	1	0	1	0	1	0	1	4
q6	2	1	0	0	0	1	1	5	—

Б.п.	q1	q2	q3	q4	q5	q6	Решение	å	Отношение
	0	-1	0	0	1	0	1	1
q4	1	2	0	1	0	0	1	5
q3	1	0	1	0	1	0	1	4	—
q6	2	1	0	0	0	1	1	5