Матричная игра двух игроков: Практическое занятие № 1, страница 3

Решить матричную игру двух игроков с нулевой суммой сведением ее к задаче линейного программирования. Использовать двойственный симплекс-метод.

Практическое занятие № 5.

«Позиционные игры»

Пример 1.

Игра состоит из трех ходов, которые делают два игрока. Первый ход делает первый игрок: он выбирает число  из множества двух чисел .

Второй ход делает второй игрок: зная, какое число  выбрано первым игроком в первом ходе, он выбирает число  из множества двух чисел .

Третий ход делает первый игрок: зная, какое число  выбрал второй игрок, и помня, какое число  он выбрал при первом ходе, выбирает число  из множества двух чисел . На этом игра заканчивается и происходит распределение выигрышей, второй игрок платит первому сумму, определенную функцией , где  задана следующим образом:

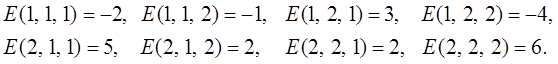
Решение:

Рассмотрим сначала мыслимые стратегии второго игрока - у него имеется возможность выбора одного из двух чисел 1 или 2, т. е. имеется две возможности. Кроме того, у него есть информация о выбранном числе  при первом ходе, следовательно, он, выбирая число , может учитывать или не учитывать эту информацию, поэтому для каждого  имеется еще два значения , т. е. всего четыре стратегии:

1-я – выбирать , не взирая на ,

2-я – выбирать , не взирая на ,

3-я – выбирать ,

4-я – выбирать , если , и выбирать , если .

Стратегия для первого игрока должна учитывать результаты сделанных ранее выборов. При каждом выборе на первом ходе может быть два выбора на втором ходе, т. е. уже имеется четыре варианта, а при каждом из этих вариантов может быть сделано два выбора, т. е. всего 8 возможных стратегий. Обозначим через  стратегию первого игрока: где  означает выбор первым игроком на первом ходе;  – выбор первым игроком на третьем ходе, если второй игрок на втором ходе выбрал число 1;  – выбор первым игроком на третьем ходе, если второй на втором ходе выбрал число 2.

Выигрыши первого игрока определяются так: пусть, например, первый игрок применяет стратегию (1, 2, 1), а второй – первую стратегию, тогда из (1, 2, 1) следует, что . Далее, второй игрок, не взирая на , выбирает , а из (1, 2, 1) следует, что первый игрок выберет . Получится выигрыш . Аналогично рассчитываются остальные выигрыши.

Приведем матрицу выигрышей первого игрока в зависимости от применяемых стратегий:

	1	2	3	4
(1, 1, 1)	(1, 1, 1) = -2	(1, 2, 1) = 3	(1, 1, 1) = -2	(1, 2, 1) = 3
(1, 1, 2)	(1, 1, 1) = -2	(1, 2, 2) = -4	(1, 1, 1) = -2	(1, 2, 2) = -4
(1, 2, 1)	(1, 1, 2) = -1	(1, 2, 1) = 3	(1, 1, 2) = -1	(1, 2, 1) = 3
(1, 2, 2)	(1, 1, 2) = -1	(1, 2, 2) = -4	(1, 1, 2) = -1	(1, 2, 2) = -4
(2, 1, 1)	(2, 1, 1) = 5	(2, 2, 1) = 2	(2, 2, 1) = 2	(2, 1, 1) = 5
(2, 1, 2)	(2, 1, 1) = 5	(2, 2, 2) = 6	(2, 2, 2) = 6	(2, 1, 1) = 5
(2, 2, 1)	(2, 1, 2) = 2	(2, 2, 1) = 2	(2, 2, 1) = 2	(2, 1, 2) = 2
(2, 2, 2)	(2, 1, 2) = 2	(2, 2, 2) = 6	(2, 2, 2) = 6	(2, 1, 2) = 2

В таблице столбцы соответствуют стратегиям второго игрока, а строки – стратегиям первого игрока: позиционная игра свелась к матричной игре двух игроков с нулевой суммой и матрицей , у которой имеется две седловые точки, отмеченные звездочкой. Оптимальная стратегия первого игрока (2, 1, 2) состоит в выборе числа  на первом ходе и числа  – на третьем ходе, равного числу ,  выбранного вторым игроком на втором ходе. У второго игрока имеется две оптимальные стратегии: первая и четвертая, т.е. выбирать , не взирая на , или выбирать , отличное от . Цена игры равна 5.