Матричная игра двух игроков: Практическое занятие № 1, страница 4

Пример 2.

Задана следующая игра:

Ход 1. Первый игрок выбирает число  из множества двух чисел .

Ход 2. Второй игрок выбирает число  из множества двух чисел , не зная значения .

Ход 3. Первый игрок выбирает число  из множества двух чисел , не зная значений ни , ни .

После того, как сделаны все три хода, второй игрок платит первому игроку сумму , заданную следующим образом:

,     ,        ,     ,

,     ,    ,    .

Решение.

Построим дерево позиционной игры

 

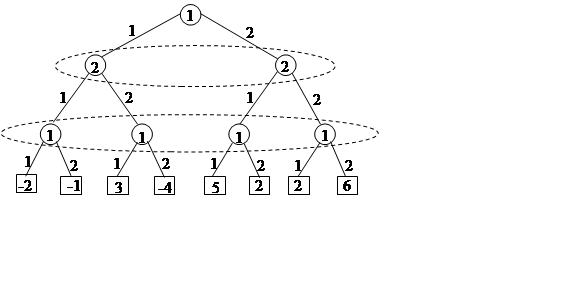Информационные множества обведены

Приведем эту игру к нормальной форме: у первого игрока имеется четыре стратегии: , , , .

У второго игрока всего две стратегии: 1-я – выбрать число 1 и 2-я стратегия – выбрать число 2. Матрица выигрышей первого игрока представлена в таблице:

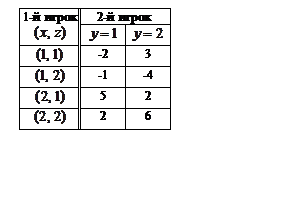В результате получилась игра порядка . Известно, что игры порядка  и  можно решать графически.

Легко убедиться, что данная игра не имеет седловой точки в чистых стратегиях:

 и ,

т.е. .

Необходимо найти такие смешанные стратегии  и  и цену игры :

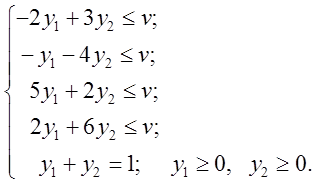
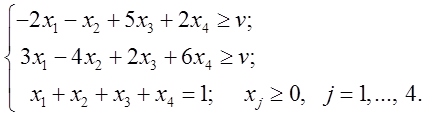
Данную задачу реши графически относительно стратегий второго игрока  и . Пусть по горизонтальной оси откладывается значение  от 0 до 1, по вертикальной – значение среднего выигрыша  первого игрока при условии, что он применяет свою чистую -ю стратегию , второй – свою смешанную стратегию . Используя соотношения (1), получим уравнения средних выигрышей второго игрока:

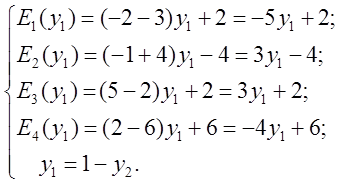
Графически  могут быть представлены так, как изображено на рисунке.

Первый игрок старается максимизировать свой выигрыш, поэтому он стремится найти .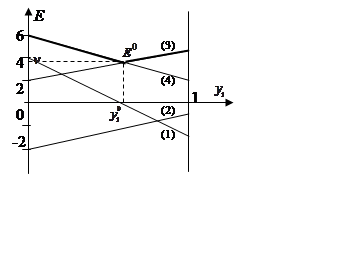

Функция  изображена жирной линией и представляет собой верхнюю границу множества ограничений. Второй игрок старается минимизировать  за счет выбора своей стратегии , т.е. величина  соответствует .

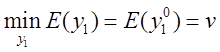Определяются такие две стратегии первого игрока и вероятность  для второго игрока, при которых достигается равенство

,

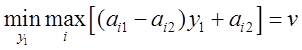или, как видно из рисунка, точку  образуют третья и четвертая стратегии первого игрока. Следовательно, ,  и для определения  и  надо составить уравнения , соответствующие этим стратегиям:

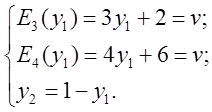
Решение этих уравнений: .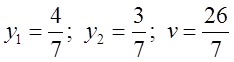

,

.

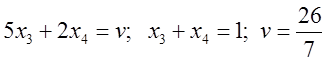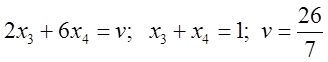В результате решения  получим стратегию первого игрока:

.

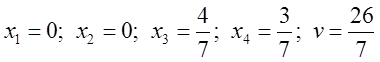Задание для самостоятельного решения:

Ход 1. Первый игрок делает выбор числа .

Ход 2. Второй игрок выбирает число , не зная значения .

Ход 3. Первый игрок выбирает число , зная  и не зная .

После того, как сделаны все три хода, второй игрок платит первому игроку сумму , заданную следующим образом:

,          ,       ,        ,

,        ,       ,        .

Построить дерево игры, привести игру к нормальной форме и решить

Практическое занятие № 6.

«Биматричные игры»

Пример 1

Для начала рассотрим пример биматричной игры в общем виде, который даст нам возможность проанализировать различные варианты решения:

Матрицы  и  равны:

,

.

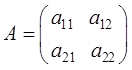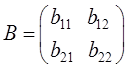Смешанные стратегии для игроков имеют вид:

,   ;

,   ,

а средние выигрыши равны:

.

.

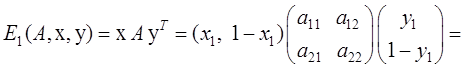
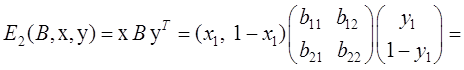
Причём

,

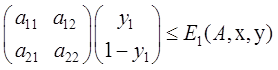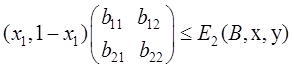
или

,

.

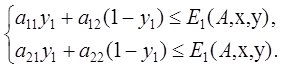
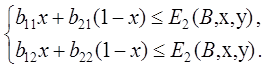
С целью упрощения положим

      ,

тогда получим

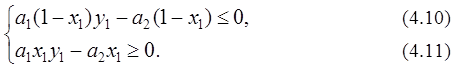
Таким образом, множество всех приемлемых стратегий для I игрока удовлетворяет этим условиям и .

Чтобы найти  рассмотрим 3 случая:

1.  Если , то .

2.  Если , то.

3.  Если , то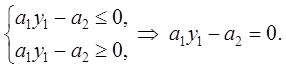

Итак, множество  решений системы состоит из

1)  всех ситуаций вида , если , ;

2)  всех ситуаций вида , если , ;

3)  всех ситуаций вида , если , .

Если , то решением является , , т.к. неравенства  выполняются при всех  и , т.е. множество приемлемых для I игрока ситуаций покрывает весь единичный квадрат.