|
Б.п. |
q1 |
q2 |
q3 |
q4 |
q5 |
q6 |
Решение |
å |
Отношение |
|
|
0 |
|
|
1 |
0 |
|
|
||
|
q2 |
|
1 |
0 |
|
0 |
0 |
|
|
|
|
q3 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
4 |
|
|
q6 |
|
0 |
0 |
|
0 |
1 |
|
|
Из оптимальной симплекс-таблицы
следует, что![]()
(q1,
q2, q3) = (0;![]() ; 1),
; 1),
а из соотношений двойственности следует, что
( p1,
p2, p3) = (![]() ; 1; 0).
; 1; 0).
Следовательно, цена игры с платёжной матрицей А1 равна
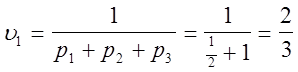 .
. 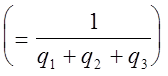 ,
,
а игры с платёжной матрицей А :
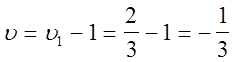 .
.
При этом оптимальные стратегии игроков имеют вид:
Х = (х1, х2, х3)
= (uр1; uр2; uр3) = 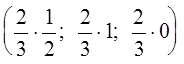 =
= 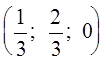
Y = (y1, y2,
y3) = (uq1; uq2; uq3) = 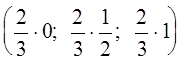 =
= 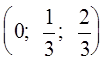 .
.
Практическое занятие № 4
«Методы решения матричных игр: решение матричной игры с помощью алгоритма двойственного симплекс метода». (Продолжение)
Решение матричной игры с произвольной ценой.

Строим математическую модель:
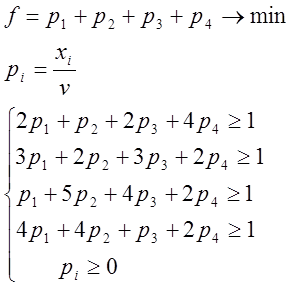
Преобразовав неравенства в уравнения, получим:
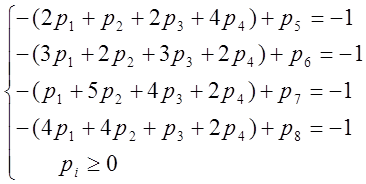
Решив, получим результат:
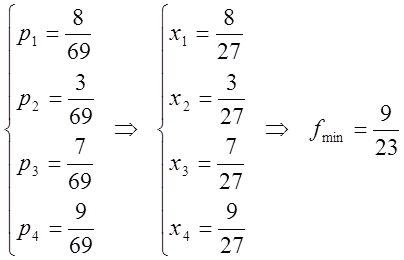
Аналогично для двойственной
задачи вводим замену 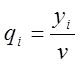 .
.
В результате:
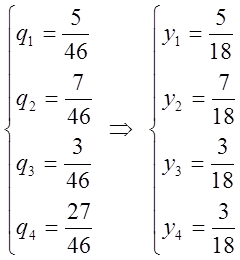
Цена игры не является произвольной величиной. Определить оптимальные смешанные стратегии и цену игры матричной игры:
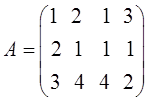 .
.
Решение
Составляем задачи:
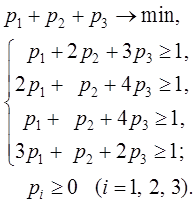
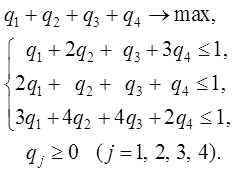
Решим эти взаимодвойственные задачи линейного программирования:
|
Переменные двойственных задач |
|
|
|
|
– |
|
|
|
|
|
|
|||
|
|
|
1 |
2 |
1 |
3 |
1 |
|
|
|
2 |
1 |
1 |
1 |
1 |
|
|
|
3 |
4 |
4 |
2 |
1 |
|
– |
-1 |
-1 |
-1 |
-1 |
0 |
|
|
Переменные двойственных задач |
|
|
|
|
– |
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
– |
|
0 |
|
|
|
|
|
Переменные двойственных задач |
|
|
|
|
– |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
Переменные двойственных задач |
|
|
|
|
– |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
 .
.
Поскольку
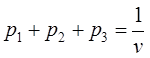 , то
, то 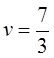 .
Переходя к исходным переменным, получим
.
Переходя к исходным переменным, получим
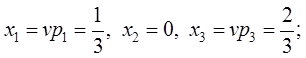
 .
.
Итак, оптимальные смешанные стратегии соответственно первого и второго игроков
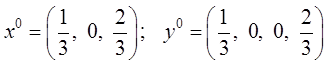 , цена игры
, цена игры 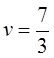 .
.
Задание для самостоятельного решения:
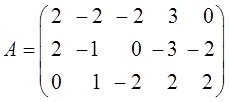 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.