Матричная игра двух игроков: Практическое занятие № 1, страница 5

Если , , то решением является либо , либо  при  (приемлемой стратегии в игре не существует).

Если , то получаем решение ;  .

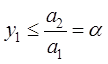Также решениями являбтся ; , и ,  

Если , то решение следующее :

, ;    , ;    , .

При этом необходимо учитывать условие .

Геометрически эти решения представлены на рис. 1 и 2.

Для II игрока исследования аналогичны. Если ввести обозначения

,

то множество приемлемых для него ситуаций состоит из:

1)  всех ситуаций вида , если , ;

2)  всех ситуаций вида , если , ; ;

3)  всех ситуаций вида , если , .

Таким образом, имеем следующие результаты:

·  если , то решение , ;

·  если , , то решение либо , либо  при  (приемлемой стратегии в игре не существует);

·  если , то решения , ;   , ;  , ;

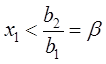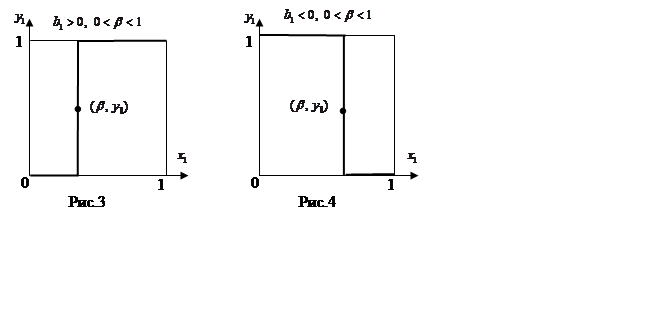·  если , то решения следующие: , ; , ;  , .

При этом необходимо учитывать, что . Геометрическое изображение представлено на рисунках 3 и 4.

Решением игры является пересечение множеств  и , т.е. те значения  и , которые являются общими для множеств  и .

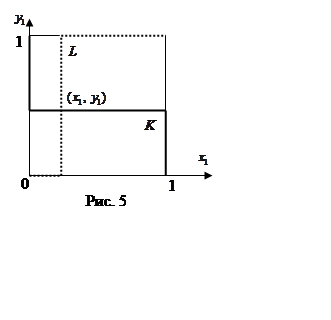
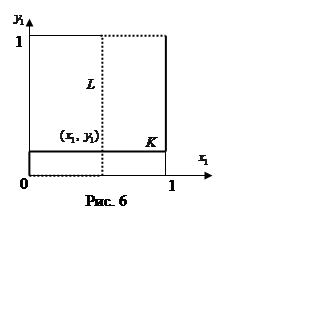
При этом графики  и  могут быть не только одинаковой (рис. 5), но и противоположной направленности (рис.6). В первом случае зигзаги имеют одну точку пересечения, а во втором – три.

 Очевидно, что  входит в смешанную стратегию II игрока хотя зависит только от выигрышей I игрока;  входит в смешанную стратегию I игрока, хотя зависит только от выигрышей II игрока.

 

Пример  2

Министерство планирует наладить выпуск одного из двух продукции на территории города. Городские власти могут принять предложение министерства или отказать. Министерство – первый игрок – имеет две стратегии: выпуск 1-ого вида продукции, выпуск 2-ого вида продукции. Город – второй игрок – имеет две стратегии: принять предложение министерства или отказать. Свои действия (стратегии) они применяют независимо друг от друга, и результаты определяются прибылью (выигрышем) согласно следующим матрицам:

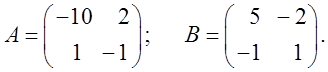
Определить оптимальные стратегии игроков и их оптимальные средние выигрыши.

Решение.

Для этой игры имеем:

,

,

.

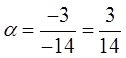Поскольку , то множество решений  имеет следующий вид:

,  где 

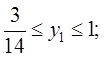
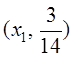,  где 

,  где  .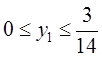

Множество  ситуаций, применяемых для первого игрока, изображено на рисунке жирной линией.

Для второго игрока имеем:

,

,

.

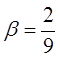Поскольку , то множество решений  имеет следующий вид:

, где

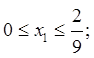
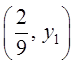, где

, где .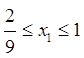

Множество  ситуаций, приемлемых для второго игрока изображено на рис. 3 пунктирной линией.

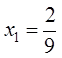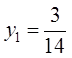Точка пересечения множеств  и  есть точка  с координатами ,  и представляет ситуацию равновесия министерства и города.

При этом их выигрыш соответственно равен

;

.

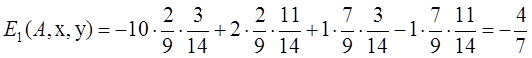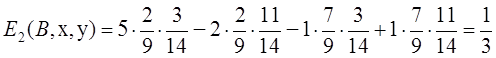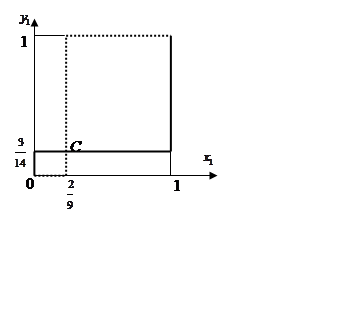
Другими словами, для получения оптимального среднего выигрыша (проигрыша) каждый из игроков должен применить следующие стратеги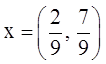и  и 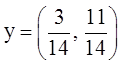 соответственно.

 

Задание для самостоятельного решения

Решить следующую биматричную игру, заданную следующими матрицами выигрыша

;                  .

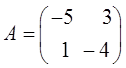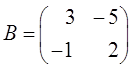Дать геометрическую интерпретацию ситуации равновесия

Практическое занятие №7.

«Бесконечные антагонистические игры»

Пример 1

Рассмотрим игру на единичном квадрате:

Решение

1)

2)

 — седловая точка в чистых стратегиях

Пример 2

Найти решение

Решение

1)

2)

Игра имеет четыре седловых точки в чистых стратегиях:

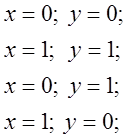
Проверим, являются ли  оптимальными стратегиями (решениями).

Если , то средний выигрыш

Определим средний выигрыш:

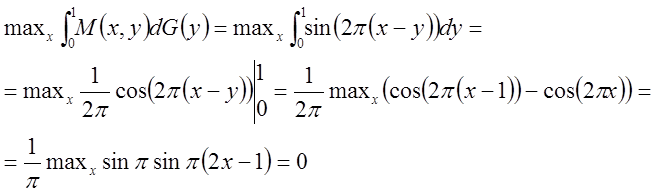
ч.т.д.

Задание для самостоятельного решения:

Решить на единичном квадрате игру