11.1 Применение линейных уравнений к колебательным движениям
11.2 Каноническая форма линейного однородного уравнения 2-го порядка
11.4 Колебательные и неколебательные решения
Ранее нами были рассмотрены
свойства линейных дифференциальных уравнений ![]() -го
порядка и даны некоторые методы их решения.
-го
порядка и даны некоторые методы их решения.
Учитывая исключительную роль, которую играют в различных приложениях линейные дифференциальные уравнения 2-го порядка, кратко ознакомимся с некоторыми их приложениями, спецификой этих уравнений и укажем главные задачи, которые можно решать с их помощью.
Положим, что материальная
точка массы ![]() движется вдоль оси
движется вдоль оси ![]() под
действием:
под
действием:
1)
силы, что притягивает ее к началу
координат , которая пропорциональна расстоянию ![]() точки
от начала координат;
точки
от начала координат;
2) силы сопротивления среды, которая пропорциональна скорости движения точки;
3)
внешней (возмущающей) силы,
которая направлена вдоль оси ![]() и в момент времени
и в момент времени ![]() равна
равна ![]() .
.
Тогда по закону Ньютона дифференциальное уравнение движения будет:
![]() или
или ![]() , (11.1)
, (11.1)
где 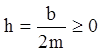 ,
, 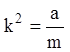 и
и 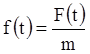 (
(![]() называют коэффициентом сопротивления,
называют коэффициентом сопротивления, ![]() – коэффициентом восстановления).
Рассмотрим отдельные случаи.
– коэффициентом восстановления).
Рассмотрим отдельные случаи.
Уравнение движения имеет вид:
![]() . (11.2)
. (11.2)
Этим уравнением описываются:
1) вертикальные
движения тела массы ![]() , подвешенного на пружине под действием
упругих сил пружины и силы тяжести;
, подвешенного на пружине под действием
упругих сил пружины и силы тяжести;
2) малые колебания маятника;
3) колебания воздуха в акустическом резонаторе и т.д.
Решаем уравнение (11.2): ![]() .
. ![]()
![]() , (11.3)
, (11.3)
или
![]() , (11.4)
, (11.4)
где ![]() называют
амплитудой колебания;
называют
амплитудой колебания;
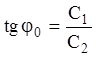 ; (11.5)
; (11.5)
![]() называют
фазой колебания;
называют
фазой колебания; ![]() – начальная фаза.
– начальная фаза.
Период колебания ![]() получим при увеличении аргумента синуса на
получим при увеличении аргумента синуса на
![]() , т.е. при увеличении
, т.е. при увеличении ![]() на
на ![]() , а,
значит,
, а,
значит, 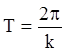 ;
;
Величину ![]() называют круговой собственной частотой
системы в отличие от обыкновенной частоты
называют круговой собственной частотой
системы в отличие от обыкновенной частоты 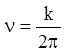 , что
представляет собой число полных колебаний за единицу времени. Постоянные
, что
представляет собой число полных колебаний за единицу времени. Постоянные ![]() и
и ![]() вполне
определяются начальными условиями:
вполне
определяются начальными условиями:
![]() ,
, ![]() .
.
Тогда уравнение движения запишется:
![]() . (11.6)
. (11.6)
Его характеристическое уравнение:
![]() , (11.7)
, (11.7)
с корнями ![]() .
.
а) если ![]() , то общее решение:
, то общее решение:
![]() . (11.8)
. (11.8)
или:
![]() , (11.9)
, (11.9)
учитывая (11.5). Как видно, амплитуда
колебания ![]() – величина переменная (
– величина переменная (![]() – начальная амплитуда). Движение точки,
описываемое формулой (11.9) называют угасающим колебанием.
– начальная амплитуда). Движение точки,
описываемое формулой (11.9) называют угасающим колебанием.
б) если же ![]() , то общее решение имеет вид
, то общее решение имеет вид
![]() . (11.10)
. (11.10)
Так как ![]() , то
, то ![]() при
при ![]() .
.
в) если ![]() , то
, то ![]() , общее
решение запишется:
, общее
решение запишется:
![]() (11.11)
(11.11)
и при ![]() ,
, ![]() .
.
Движения, описываемые
формулами (11.10)-(11.11) называют апериодичными угасающими движениями.
С возрастанием ![]() отклонение
отклонение ![]() асимптотически приближается к нулю. Все рассмотренные
выше движения называют собственными колебаниями.
асимптотически приближается к нулю. Все рассмотренные
выше движения называют собственными колебаниями.
Положим, что внешняя сила периодическая (в приложениях это случается очень часто), тогда уравнение (11.1) запишется
![]() ,
, ![]() . (11.12)
. (11.12)
Корни характеристического
уравнения ![]() ,
, ![]() , поэтому
, поэтому
![]() и при нахождении
и при нахождении ![]() будем
рассматривать два случая: 1)
будем
рассматривать два случая: 1) ![]() ; 2)
; 2) ![]() .
.
В случае ![]() (собственная частота внешней силы отлична
от собственной частоты свободных колебаний) частное решение ищем в виде
(собственная частота внешней силы отлична
от собственной частоты свободных колебаний) частное решение ищем в виде ![]() . Ищем
. Ищем ![]() и
и ![]() . Для этого находим
. Для этого находим ![]() ,
,
![]() . Подставляем в (11.12):
. Подставляем в (11.12):
![]() ,
,
Откуда:
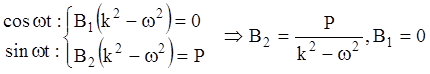 .
.
Тогда: 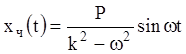 и общее решение уравнения (11.12):
и общее решение уравнения (11.12):
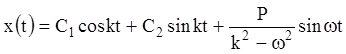 , или (11.13)
, или (11.13)
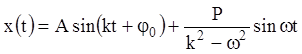 . (11.14)
. (11.14)
Первый
член решения (11.14) описывает собственные колебания, второй – вынужденные.
Вынужденные колебания имеют собственную частоту внешней силы, а их амплитуда
определяется амплитудой возмущающей силы и параметрами системы. Свободные
колебания происходят с собственной частотой ![]() .
Значит, колебания происходят с двумя частотами –
.
Значит, колебания происходят с двумя частотами – ![]() и
и ![]() , и поэтому результирующее колебание не
будет гармоническим. Из формулы (11.14) следует, что амплитуда вынужденных
колебаний очень велика, если
, и поэтому результирующее колебание не
будет гармоническим. Из формулы (11.14) следует, что амплитуда вынужденных
колебаний очень велика, если ![]() мало отличается от
мало отличается от ![]() и бесконечно возрастает, если
и бесконечно возрастает, если ![]() . В реальной системе колебания с
бесконечной амплитудой невозможны. При
. В реальной системе колебания с
бесконечной амплитудой невозможны. При ![]() формула
(11.14) вообще теряет смысл. Возникает вопрос, какой же характер колебаний при
формула
(11.14) вообще теряет смысл. Возникает вопрос, какой же характер колебаний при ![]() ? В этом случае частное решение неоднородного
уравнения (11.12) ищут в виде:
? В этом случае частное решение неоднородного
уравнения (11.12) ищут в виде:
![]()
Находим ![]() и
и ![]() ,
подставляя
,
подставляя ![]() в (11.12) и приравнивая коэффициенты при
в (11.12) и приравнивая коэффициенты при ![]() и
и ![]() :
: 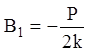 и
и ![]() . Тогда
общее решение (11.12) запишется:
. Тогда
общее решение (11.12) запишется:
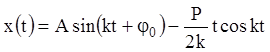 . (11.15)
. (11.15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.