Практичне заняття №5-6
Тема заняття: «Матричний метод ЛОС із постійними коефіцієнтами».
I. Перевірка виконаного домашнього завдання.
II. Теоретичне опитування:
1. Який вид має ЛОС із постійними коефіцієнтами в матричній формі?
2. У чому ідея «Матричного методу» розв'язання ЛОС?
3.
Як за допомогою матричних рядів установити вид інтегральної матриці ![]() ЛОС?
ЛОС?
4.
Як шукати інтегральну матрицю ![]() ЛОС?
ЛОС?
5.
Що це за формула ![]() і як находяться її компоненти?
і як находяться її компоненти?
III. Розв'язання задач:
Розв’язати
ОЛС ![]() матричним методом, якщо
матричним методом, якщо
I. Корені характеристичного рівняння дійсні й різні:
1. 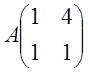 .
.
Розв'язання: 1) Записуємо матрицю ![]() , транспонуючи матрицю
, транспонуючи матрицю ![]()
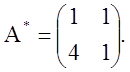
2) Приводимо
матрицю ![]() до канонічної жорданової формі. Для цього
записуємо характеристичне рівняння й знаходимо характеристичні числа
до канонічної жорданової формі. Для цього
записуємо характеристичне рівняння й знаходимо характеристичні числа ![]() тобто
тобто 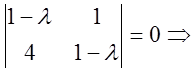
![]()
Простим корінням характеристичного рівняння відповідають прості
елементарні дільники матриці: ![]() ,
, ![]() У силу цього, нормальна жорданова форма
матриці A має вигляд:
У силу цього, нормальна жорданова форма
матриці A має вигляд:
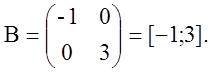
З формули ![]() витікає, що
витікає, що ![]() або в розгорнутому виді, поклавши
або в розгорнутому виді, поклавши 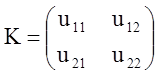 , знаходимо:
, знаходимо:
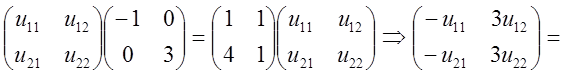
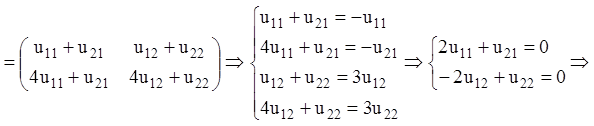
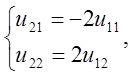
звідки, поклавши, ![]()
![]() знаходимо
знаходимо ![]()
![]()
Тоді матриця:
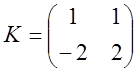
і зворотна матриця: 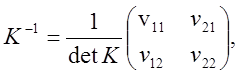 де
де ![]() –
алгебраїчні доповнення елементів матриці
–
алгебраїчні доповнення елементів матриці ![]() має
вигляд:
має
вигляд: 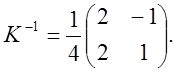
3) Знаходимо інтегральну матрицю:
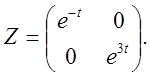
4) Знаходимо інтегральну матрицю вихідної системи:
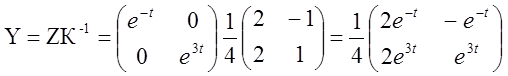
або
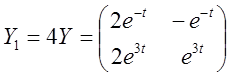
5) Тоді загальне розв'язання вихідної системи запишеться у вигляді лінійної комбінації:
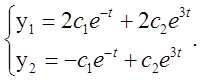
2. 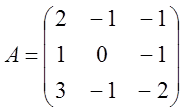 3.
3.
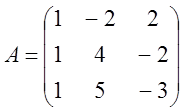 4.
4. 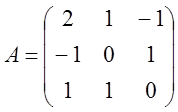 .
.
II. Корені характеристичного рівняння комплексні:
1. 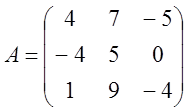 .
.
Розв'язання: 1) Складаємо матрицю 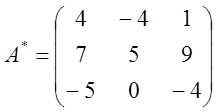
2) 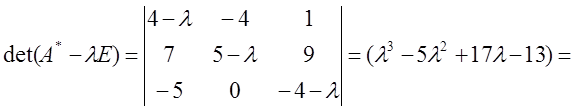
![]()
Корені характеристичного многочлена ![]() –
прості. Елементарними дільниками в полі комплексних чисел будуть
–
прості. Елементарними дільниками в полі комплексних чисел будуть ![]() , а це значить, що жорданова форма матриці
, а це значить, що жорданова форма матриці ![]() має вигляд:
має вигляд:
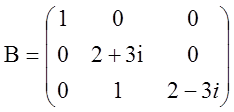 .
.
Знаходимо відразу матрицю ![]() з рівності
з рівності ![]()
Думаючи 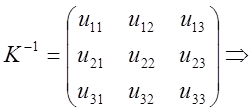
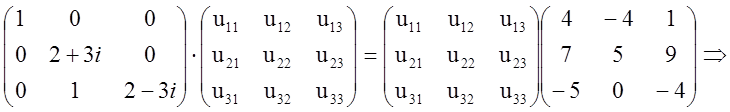
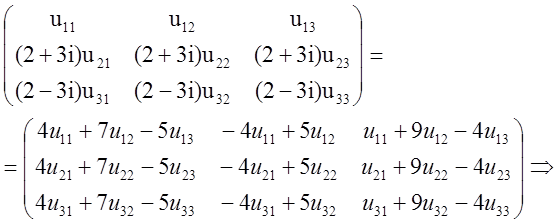
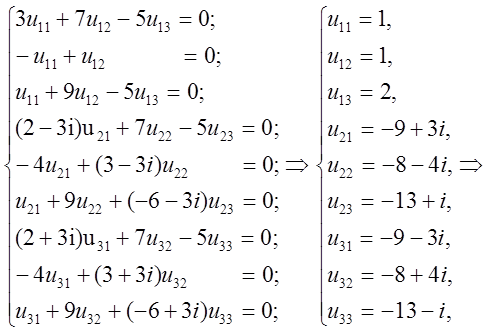
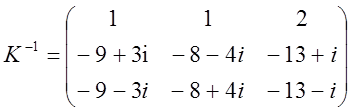 .
.
3) Знаходимо інтегральну матрицю:
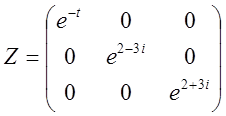
4) 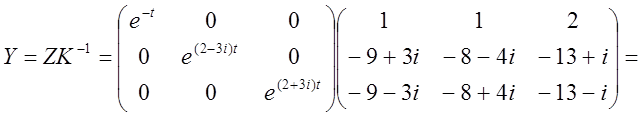
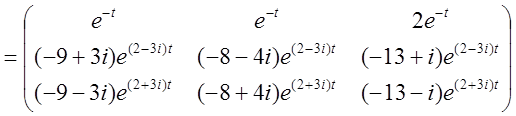
Замінимо в інтегральній матриці Y комплексне розв'язання відповідної дійсним, відокремлюючи дійсні й мнимі частини, з огляду на що:
![]()
Тоді:
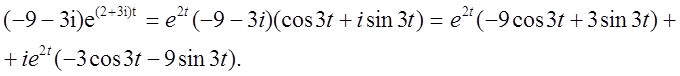
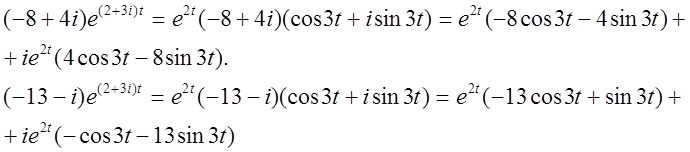
і дійсна інтегральна матриця запишеться:
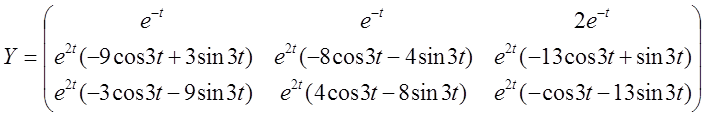
Тоді загальне розв'язання в дійсній формі запишеться:
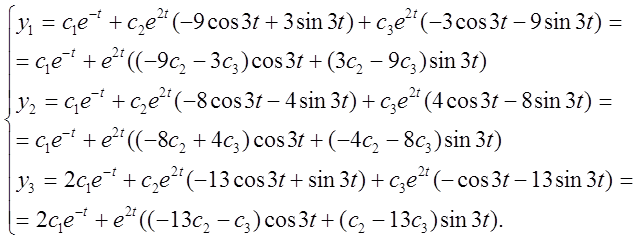
2. 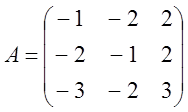 3.
3. 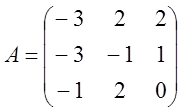 4.
4. 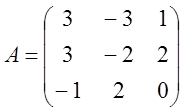
III. Корені характеристичного рівняння кратні:
1. 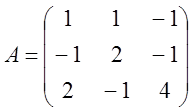 .
.
Розв'язання: 1) 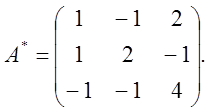
2) 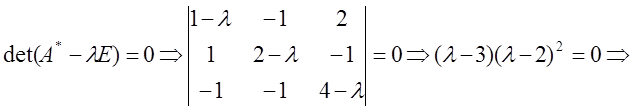
![]() Ранг
матриці
Ранг
матриці 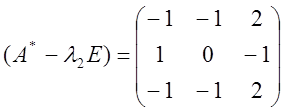 дорівнює
дорівнює ![]() , тому
кількість елементарних дільників, що відповідають цьому характеристичному числу
дорівнює
, тому
кількість елементарних дільників, що відповідають цьому характеристичному числу
дорівнює ![]() , а це значить, що елементарні дільники
мають вигляд
, а це значить, що елементарні дільники
мають вигляд ![]() і жорданова форма матриці
запишеться:
і жорданова форма матриці
запишеться:
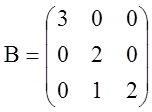 .
.
Знаходимо матрицю ![]() з рівності
з рівності ![]() :
:
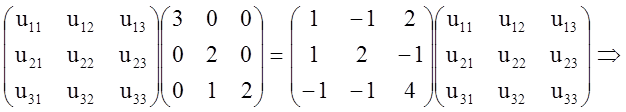
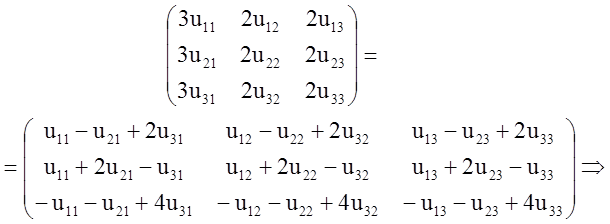
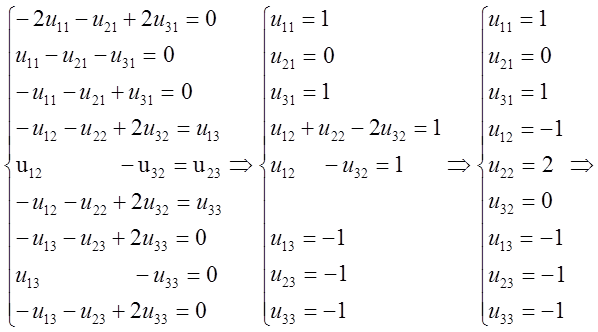
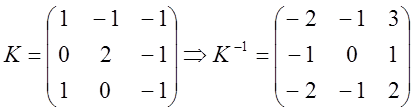
3) Знаходимо інтегральну матрицю: 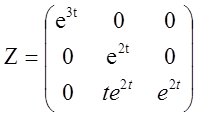
4) 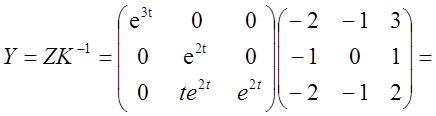
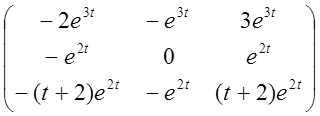
5) Загальне розв'язання запишеться:
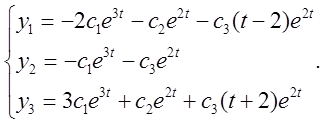
2. 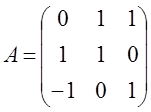 3.
3. 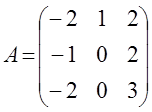 4.
4.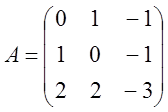 5.
5. 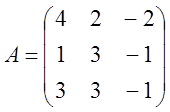 6.
6. 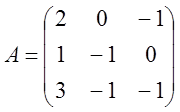
IV. Домашнє завдання:
1. Підготувати теоретичний матеріал по темі «Метод Ейлера розв'язання ЛОС із постійними коефіцієнтами».
2 Розв’язати вдома задачі, що залишилися
3. Принести виконану частину індивідуального завдання по темі.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.