Линейные неоднородные уравнения. Методы решения неоднородных линейных уравнений

ЛЕКЦИЯ №9.

Тема: ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ

ПЛАН

9.1 Неоднородные линейные уравнения

9.2 Методы решения неоднородных линейных уравнений

9.2.1 Метод вариации произвольных постоянных (метод Лагранжа)

9.2.2 Решение неоднородных линейных дифференциальных уравнений с постоянными коэффициентами и со специальной правой частью

9.1 Неоднородные линейные уравнения

Рассмотрим неоднородное линейное дифференциальное уравнение (сокращение – НЛДУ):

   (9.1)

или:

,                                              (9.2)

где  и  – непрерывные в некотором интервале  функции.

Однородное линейное уравнение с теми же коэффициентами :

                           (9.3)

или:

,                                        (9.4)

называют соответствующим однородным уравнением (сокращенно СОЛДУ).

Между общим решением НЛДУ (9.1) и общим решением СОЛДУ (9.2) существует связь, устанавливаемая теоремой.

Т е о р е м а. Общее решение НЛДУ (9.1)  равно сумме двух решений , где  – СОДУ (2) и  – любое частное решение НЛДУ (9.1), т.е.:

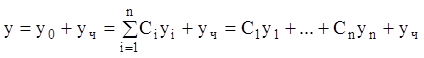.                 (9.5)

Д о к а з а т е л ь с т в о. Т. к. - частное решение уравнения (9.1), а  – общее решение уравнения (9.3), то

                          (9.6)

и

.                            (9.5)

Рассмотрим функцию (9.5) . Подставляя (9.5) в (9.1), и учитывая свойства линейности линейного оператора, получаем  или . Откуда в силу (9.6) и (9.5) получаем , т.е. , т.е. функция (9.5) является решением НЛДУ (9.1).

Покажем, что функция (9.5) является общим решением НЛДУ (9.1), т.е. при любых начальных условиях

,        (9.6)

где  – заданные числа, можно так подобрать произвольные постоянные  формулы (9.5), чтобы выполнялись условия (9.6). В самом деле, из (9.6) с учетом (9.5) строим систему линейных алгебраических уравнений для нахождения :

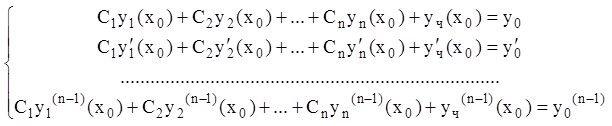
или:

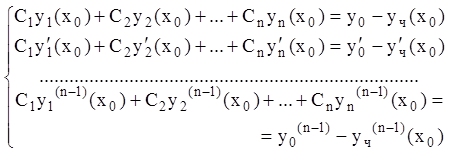.       (9.7)

Эта система имеет единственное решение т.к. ее главный определитель

,

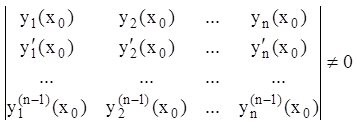как определитель Вронского фундаментальной системы решений ОЛДУ (9.3) .

Таким образом, функция (9.5) является общим решением уравнения (9.1), ч.т.д.

По предыдущей теореме задача интегрирования уравнения (9.1) сводится к решению двух задач:

1)   нахождение общего решения СОЛДУ;

2)   нахождение любого частного решения НЛДУ.

Для нахождения частного решения НЛДУ уравнения (9.1) используются разные способы. Рассмотрим так называемый «метод вариаций произвольных постоянных».

9.2 Методы решения неоднородных линейных уравнений

9.2.1 Метод вариации произвольных постоянных (метод Лагранжа)

Допустим, что нам известно общее решение СОЛДУ (9.3):

.            (9.8)

Будем искать частное решение уравнения (9.1) в таком же виде как и общее решение СОЛДУ (9.3), заменяя произвольные постоянные  некоторыми непрерывно дифференцируемыми функциями от , т.е. положим:

.               (9.9)

Подберем  так, чтобы функция (9.9) была решением уравнения (9.1). Для нахождения  неизвестных функций нам необходимо  уравнений. Одно уравнение получим из условия, что функция (9.9) удовлетворяет уравнению (9.1), а остальные  найдем следующим образом. Дифференцируя функцию (9.9) по ,

накладываем на  следующие условия

.                   (9.10)

Тогда:

.                (9.11)

Вычисляем :

и накладываем снова на  условия

.                 (9.12)

Тогда:

                (9.13)

и т.д. ...

Продолжая вычисление производных и накладывая условия, находим :

 

.

Снова условие:

,            (9.14)

тогда:

        (9.15)

и:

      .  (9.16)

Подставим найденные значения  в уравнение (9.1). Для этого умножим равенства (9.9), (9.11), (9.13), (9.15), (9.16) соответственно на , сложим почленно и приравняем правую часть полученного равенства правой части уравнения (9.1):

 .   (9.16)

Так как , как решения уравнения (9.3), то последнее запишется:

.      (9.17)

Таким образом, для определения  получаем следующую систему уравнений (9.10, 9.12, 9.14, 9.16):

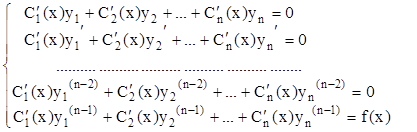. (9.18)

Это алгебраическаялинейная неоднородная система, имеющая единственное решение, т.к. ее определитель является определителем Вронского фундаментальной системы решений  и  Решив ее, получаем:

,

где  – непрерывные на  функции. Откуда

.                  (9.19)

Подставив найденные значения  в (9.9) получаем искомое решение уравнения (9.1). Поставленная задача решена.

Изложенный метод вариации произвольных постоянных связывается в литературе с именем Лагранжа, который опубликовал его в 1774 году. Но следует отметить, что его применяли и раньше (1740г.) Л. Эйлер и Д. Бернулли.

П р и м е р  1. Решить уравнение

Р е ш е н и е. Ищем общее решение СОЛДУ;

 ,. Тогда частное решение НЛДУ ищем в виде . Для нахождения  и  составляем систему (9.18):

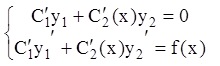 или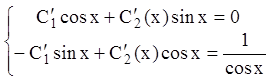

Решая систему относительно  и , находим  

Интегрируя, находим  и частное решение .

Тогда общее решение исходного уравнения:

.