Линейные дифференциальные уравнения высших порядков

ЛЕКЦИЯ №8.

Тема: 8. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

ПЛАН

8.1 Основные понятия. Свойства линейных уравнений и их решений

8.2. Понижение порядка линейного однородного уравнения

8.3 Линейные однородные дифференциальные уравнения с постоянными коэффициентами

8.1 Основные понятия. Свойства линейных уравнений и их решений

Линейным дифференциальным уравнениемn-го порядка называют уравнение, линейное относительно неизвестной функции и ее производных. Его общий вид:

,                       (8.1)

где коэффициенты уравнения  - свободный член уравнения.

Эти уравнения широко используются в практике научных исследований и это наиболее исследованный класс уравнений.

Левую часть уравнения (8.1) называют линейным дифференциальным выражением n-го порядка и обозначают L(y).

Линейным дифференциальным оператором n-го порядка называют оператор

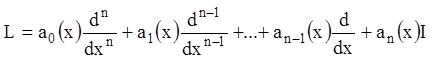,                             (8.2)

где - тождественный оператор. Согласно этому уравнение (8.1) можно записать:

.                                                          (8.3)

При  уравнение (8.1) или (8.3) называют однородным линейным уравнением, в противном случае – неоднородным. Очевидно, что любое однородное уравнение имеет тривиальное решение .

Если в (8.1) или (8.3) , то разделив уравнение на получаем приведенное линейное уравнение:

,                         (8.4)

однородное, если  и неоднородное при .

Замечания:

1) в случае приведенного линейного уравнения (8.4) под линейным дифференциальным оператором -го порядка будем понимать:

,

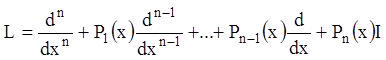где  - заданные непрерывные в области  функции,  – тождественный оператор. Тогда приведенное линейное уравнение (8.4) запишется

.

2) очевидно, что разрешив уравнение (8.4) относительно , получим уравнение:

,

правая часть которого непрерывна на  и будет иметь ограниченные производные по переменным . Тогда по теореме существования и единственности уравнение (8.4) будет иметь единственное решение , удовлетворяющее начальным условиям

,

где  – любая точка , а  – любые заданные числа. Особых решений линейное уравнение не имеет.

Рассмотрим основные свойства линейных уравнений и их решений.

Предварительно установим основные свойства линейного дифференциального оператора:

1) постоянный множитель выносится за знак линейного дифференциального оператора:

.                                                    (8.5)

Действительно,

 

2) линейный дифференциальный оператор, примененный к сумме двух функций  и , равен сумме результатов применения того же оператора к каждой функции в отдельности:

.                                       (8.6)

Действительно,

.

Следствием свойств 1) и 2) является свойство:

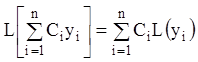, .                                     (8.7)

Используя свойства линейного оператора , докажем ряд теорем о решениях линейного однородного уравнения.

Т е о р е м а 1. Если  является решением линейного однородного уравнения , то и , где  – произвольная постоянная, является решением того же уравнения.

Д о к а з а т е л ь с т в о. Дано. Докажем, что . Пользуясь свойством 1) оператора, получим:

, ч.т.д.                                              (8.8)

Т е о р е м а 2. Если и  являются решениями линейного однородного уравнения , то сумма  тоже является решением того же уравнения.

Д о к а з а т е л ь с т в о. Дано  и . Докажем, что . Пользуясь свойством 2) оператора , получим:

, ч.т.д.                                  (8.9)

С л е д с т в и е  т е о р е м  1  и  2. Линейная комбинация с произвольными постоянными коэффициентами ( – произвольные коэффициенты) 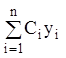 решений  линейного однородного уравнения  является решением того же уравнения.

Т е о р е м а  3. Если линейное однородное уравнение  с действительными коэффициентами  имеет комплексное решение , то действительная часть этого решения и его мнимая часть в отдельности являются решениями того же однородного уравнения.

Д о к а з а т е л ь с т в о. Дано . Надо доказать, что  и . Пользуясь свойствами 1) и 2) оператора , получаем:

.                                     (8.10)

Так как комплексная функция действительного переменного обращается тождественно в нуль тогда, и только тогда, когда ее действительная и мнимая части тождественно равны нулю, то  и , ч.т.д.

П р и м е р  1. Уравнение  имеет комплексное решение , в чем легко убедиться непосредственно подстановкой. Вместе с тем, его действительная  и мнимая части тоже являются решениями этого же уравнения.

Рассмотрим еще два общих свойства линейного уравнения.

Т е о р е м а  4. Линейное уравнение  остается линейным при любой замене независимой переменной , где  - произвольная  - раз дифференцируемая функция в интервале  и , причем .

Д о к а з а т е л ь с т в о. Вычислим производные:

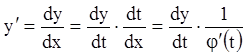,                                                       (8.11)