 , (11.30)
, (11.30)
называют самосопряженным.
Докажем, что любое однородное линейное уравнение 2-го порядка
![]() , (11.31)
, (11.31)
коэффициенты которого непрерывные
функции на ![]() , можно привести к самосопряженному виду,
умножив его на некоторый множитель
, можно привести к самосопряженному виду,
умножив его на некоторый множитель ![]() .
.
Действительно, умножив
(11.31) на ![]()
![]()
и будем подбирать ![]() так, чтобы коэффициент при
так, чтобы коэффициент при ![]() был равен производной от коэффициента при
был равен производной от коэффициента при ![]() , т.е.
, т.е.
![]() (11.32)
(11.32)
или ![]() ,
,
или ![]() ,
,
или 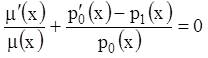 , или
, или 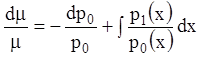 ,
,
или ![]()
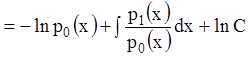 . Положив
. Положив ![]() ,
получим:
,
получим:
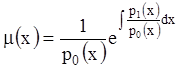 (11.33)
(11.33)
Т.о. умножив уравнение
(11.31) на полученное ![]() , получим:
, получим:
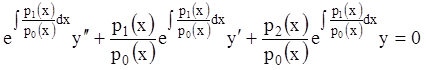
или:
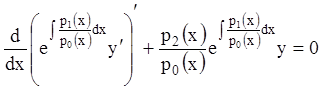 , (11.34)
, (11.34)
т.е. получим уравнение (11.30), где 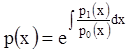 и
и 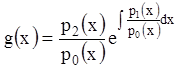 .
Отметим при этом:
.
Отметим при этом: ![]() и
и ![]() –
непрерывные на
–
непрерывные на ![]() функции, причем
функции, причем ![]() .
.
П р и м е р. Приведем к самосопряженному виду уравнение цилиндрических
функций ![]() ,
, ![]() .
.
Р е ш е н и е. По формуле
(11.33) 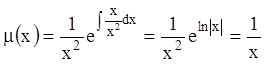 . Умножив на
. Умножив на 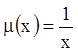 ,
получим:
,
получим: 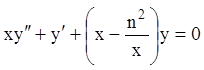 или
или 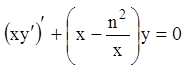 –
самосопряженная форма уравнения.
–
самосопряженная форма уравнения.
Пусть однородное линейное дифференциальное уравнение 2-го порядка:
![]() , (11.21)
, (11.21)
где ![]() и
и
![]() – непрерывные функции в рассматриваемом интервале
– непрерывные функции в рассматриваемом интервале
![]() . Если
. Если ![]() , и
заданы начальные условия
, и
заданы начальные условия
![]() , (11.35)
, (11.35)
то по теореме существования и единственности решения задачи Коши есть только одно решение уравнения (11.21), которое удовлетворяет условиям (11.35). В частности, если
![]() и
и ![]() , (11.36)
, (11.36)
то искомое решение будет тривиальным:
![]() , т.к. только оно удовлетворяет условиям
(11.21), (11.36).
, т.к. только оно удовлетворяет условиям
(11.21), (11.36).
В теории и на практике,
особенно при физических исследованиях, очень важно знать: имеет ли решение ![]() данного уравнения нули, принадлежащие рассматриваемому
промежутку
данного уравнения нули, принадлежащие рассматриваемому
промежутку ![]() , или не имеет, а если имеет, то сколько
их. Впервые эта проблема была исследована французским математиком Штурмом в
1836г.
, или не имеет, а если имеет, то сколько
их. Впервые эта проблема была исследована французским математиком Штурмом в
1836г.
Перед рассмотрением основных теорем Штурма, рассмотрим два примера и введем некоторые новые понятия.
Пусть имеем два уравнения
![]() и
и ![]() ,
,
где ![]() .
.
Решение первого из них:
![]() , (11.37)
, (11.37)
а второго –
![]() или
или ![]() . (11.38)
. (11.38)
Анализ решений (11.37),
(11.38) показывает, что между ними существуют большие различия. В то время, как
каждое частное решение, получаемое из (11.37), может иметь только один корень
при ![]() , то каждое частное решение уравнения,
полученного из (11.38), будет иметь бесконечное число корней при
, то каждое частное решение уравнения,
полученного из (11.38), будет иметь бесконечное число корней при ![]() , расстояние между которыми равно
, расстояние между которыми равно ![]() . Значит, любое решение второго уравнения
будет иметь хотя бы два корня на любом промежутке, длина которого больше, чем
. Значит, любое решение второго уравнения
будет иметь хотя бы два корня на любом промежутке, длина которого больше, чем ![]() .
.
Решение дифференциального
уравнения 2-го порядка называют колебательным на промежутке ![]() , если оно обращается в
нуль внутри этого промежутка не менее двух раз. В противном случае решение
называют неколебательным на
, если оно обращается в
нуль внутри этого промежутка не менее двух раз. В противном случае решение
называют неколебательным на![]() . Т.о.
все решения первого уравнения – неколебательные на любом конечном промежутке, а
решения второго – колебательные на любом интервале длиной больше
. Т.о.
все решения первого уравнения – неколебательные на любом конечном промежутке, а
решения второго – колебательные на любом интервале длиной больше ![]() . Заметим, что при
. Заметим, что при ![]() оба
уравнения будут иметь вид
оба
уравнения будут иметь вид ![]() , решения которого
, решения которого ![]() являются, очевидно, неколебательными.
являются, очевидно, неколебательными.
Т.о., делаем вывод, что
уравнение ![]() имеет неколебательные решения в любом
промежутке, если
имеет неколебательные решения в любом
промежутке, если ![]() , и колебательные в достаточно
большом промежутке, если
, и колебательные в достаточно
большом промежутке, если ![]() .
.
Оказывается, что условие ![]() для неколебательных решений распространяется
и на случай, если
для неколебательных решений распространяется
и на случай, если ![]() , т.е. на случай уравнений 2-го
порядка с переменными коэффициентами. Рассмотрим уравнение 2-го порядка, взятое
в канонической форме:
, т.е. на случай уравнений 2-го
порядка с переменными коэффициентами. Рассмотрим уравнение 2-го порядка, взятое
в канонической форме:
![]() . (11.39)
. (11.39)
К нему, как показано ранее,
приводятся любые линейные уравнения 2-го порядка ![]() путем
замены
путем
замены ![]() .
.
Будем рассматривать только те
промежутки, где ![]() . Тогда, т.к.
. Тогда, т.к. 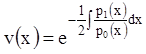 , функции
, функции ![]() и
и ![]() будут иметь одни и те же корни.
будут иметь одни и те же корни.
Имеет место теорема.
Т е о р е м а. Если на
промежутке ![]() функция
функция ![]() непрерывна
и удовлетворяет неравенству
непрерывна
и удовлетворяет неравенству ![]() при
при ![]() , то любое ненулевое решение уравнения
(11.39) будет неколебательным.
, то любое ненулевое решение уравнения
(11.39) будет неколебательным.
Д о к а з а т е л ь с т в о (
о т п р о т и в н о г о ). Допустим противоположное, что существует какое-то
решение ![]() уравнения (11.39), которое имеет хотя бы
два нуля
уравнения (11.39), которое имеет хотя бы
два нуля ![]() и
и ![]() на
на ![]() , т.е. является колебательным на
, т.е. является колебательным на ![]() . Для определенности положим, что
. Для определенности положим, что ![]() и
и ![]() . Допустим
далее, что между
. Допустим
далее, что между ![]() и
и ![]() решение
решение
![]() не имеет нулей. Тогда
не имеет нулей. Тогда ![]() как непрерывная функция будет сохранять
знак между двумя соседними корнями
как непрерывная функция будет сохранять
знак между двумя соседними корнями ![]() и
и ![]() (для определенности положим, например,
(для определенности положим, например, ![]() при
при ![]() ). Тогда
правее т.
). Тогда
правее т. ![]() т.к.
т.к. ![]() возрастает
правее от т.
возрастает
правее от т. ![]() и
и ![]() . Тогда
уравнение (11.39) запишем в виде
. Тогда
уравнение (11.39) запишем в виде
![]() .
.
Т.к. по условию теоремы ![]() и
и ![]() , то
, то ![]() при
при ![]() .
Поэтому
.
Поэтому ![]() не убывает на
не убывает на ![]() , т.е.
, т.е.
![]() при
при ![]() .
.
По формуле конечных приращений функции будем иметь:
![]() , где
, где ![]() .
.
Но левая часть последнего равенства равна нулю, а правая положительная. Значит сделанное допущение о существовании хотя бы 2-х корней неверно, т.е. решение будет неколебательным, ч. т .д.
В ы в о д: Если ![]() для всех значений
для всех значений ![]() ,
то решение уравнения (11.39) неколебательные в любом конечном промежутке,
значит, каждая интегральная кривая пересекает ось
,
то решение уравнения (11.39) неколебательные в любом конечном промежутке,
значит, каждая интегральная кривая пересекает ось ![]() не
более одного раза.
не
более одного раза.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.