Второй член показывает, что
при возрастании ![]() амплитуда вынужденного колебания
возрастает неограниченно. Это так называемое явление резонанса, которое
имеет место при совпадении собственной частоты и частоты возмущающей силы
амплитуда вынужденного колебания
возрастает неограниченно. Это так называемое явление резонанса, которое
имеет место при совпадении собственной частоты и частоты возмущающей силы ![]() .
.
Полагая снова, что
возмущающая сила ![]() , получим уравнения движения в
виде
, получим уравнения движения в
виде
![]() . (11.16)
. (11.16)
Полагая, что колебания –
угасающие, т.е. ![]() , положим, как и раньше,
, положим, как и раньше, ![]() , и корни характеристического уравнения
будут
, и корни характеристического уравнения
будут ![]() , получим:
, получим:
![]() . (11.17)
. (11.17)
Находим ![]() и
и ![]() :
:
![]() ,
, ![]() .
.
Подставляя их значения в
(11.16) и приравнивая коэффициенты при ![]() и
и ![]() получаем:
получаем:
 ,
, 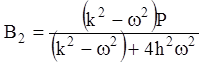 .
.
Поэтому искомое частное решение запишется:
 , (11.18)
, (11.18)
а общее:
 . (11.19)
. (11.19)
Из (11.19) следует, что, если
![]() достаточно мало, а
достаточно мало, а ![]() –
близко к
–
близко к ![]() , то выражение
, то выражение ![]() близко
к нулю, и амплитуда вынужденных колебаний резко возрастает. Наблюдаем снова
явление резонанса. Но тут существенное отличие: колебания хоть и большие, но не
возрастают до бесконечности, как в случае отсутствия сопротивления. В
сооружениях и машинах явление резонанса играет очень негативную роль:
увеличение амплитуды колебаний порождает увеличение напряжения материала, а это
может привести к разрушению сооружения или машины. Значит, проектируя части той
или иной машины, нужно определить частоты их собственных колебаний так, чтобы
предотвратить явление резонанса.
близко
к нулю, и амплитуда вынужденных колебаний резко возрастает. Наблюдаем снова
явление резонанса. Но тут существенное отличие: колебания хоть и большие, но не
возрастают до бесконечности, как в случае отсутствия сопротивления. В
сооружениях и машинах явление резонанса играет очень негативную роль:
увеличение амплитуды колебаний порождает увеличение напряжения материала, а это
может привести к разрушению сооружения или машины. Значит, проектируя части той
или иной машины, нужно определить частоты их собственных колебаний так, чтобы
предотвратить явление резонанса.
Пусть имеем линейное однородное уравнение 2-го порядка:
![]() , (11.20)
, (11.20)
где ![]() –
непрерывные в заданном интервале
–
непрерывные в заданном интервале ![]() функции, причем
функции, причем ![]() . Разделив на
. Разделив на![]() , получим:
, получим:
![]() (11.21)
(11.21)
и проведем замену:
![]() (11.22)
(11.22)
где ![]() –
новая искомая функция. Подставим (11.22) в (11.21), предварительно вычислив
–
новая искомая функция. Подставим (11.22) в (11.21), предварительно вычислив ![]() и
и ![]() :
: ![]() ;
; ![]()
![]()
![]() или
или
![]() . (11.23)
. (11.23)
Подберем функцию ![]() так, чтобы
так, чтобы ![]() , т.е.
, т.е.
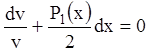 или
или 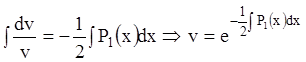 .
.
Подставляем найденное
значение ![]() в (11.23), предварительно вычислив
в (11.23), предварительно вычислив 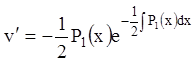 ,
,  ;
тогда
;
тогда

 или
или
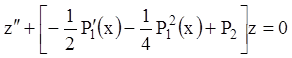
или, если положим
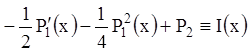 , (11.24)
, (11.24)
будем иметь окончательно:
![]() . (11.25)
. (11.25)
Уравнение (11.25) называют канонической
формой уравнения (11.21). Функция ![]() называется
инвариантом уравнения (11.21), т.к. она не меняет своего вида при любых
подстановках вида (11.22). Очевидно, если уравнение (11.25) приводится к
квадратурам, то к квадратурам приводится и уравнение (11.21). Это будет иметь
место, например, тогда, когда
называется
инвариантом уравнения (11.21), т.к. она не меняет своего вида при любых
подстановках вида (11.22). Очевидно, если уравнение (11.25) приводится к
квадратурам, то к квадратурам приводится и уравнение (11.21). Это будет иметь
место, например, тогда, когда ![]() , или
, или 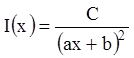 . В первом случае уравнение (11.25) будет
линейным с постоянными коэффициентами, а во втором – уравнением Лагранжа.
Отметим, что для линейного уравнения 2-го порядка с постоянными коэффициентами:
. В первом случае уравнение (11.25) будет
линейным с постоянными коэффициентами, а во втором – уравнением Лагранжа.
Отметим, что для линейного уравнения 2-го порядка с постоянными коэффициентами:
![]()
инвариант ![]() представляет
собой
представляет
собой  дискриминант характеристического уравнения
дискриминант характеристического уравнения
![]() , взятый с противоположным знаком.
, взятый с противоположным знаком.
Из равенства (11.23) видно,
что функцию ![]() можно подобрать и другим способом, а
именно так, чтобы она была решением уравнения (11.21). При таком подборе
можно подобрать и другим способом, а
именно так, чтобы она была решением уравнения (11.21). При таком подборе ![]() , обозначив
, обозначив ![]() и
положив
и
положив ![]() , из (11.23) получим:
, из (11.23) получим: ![]() , или, разделив на
, или, разделив на ![]() :
:
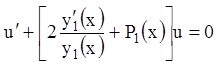 или
или 
![]()
![]()
Проинтегрировав, получаем 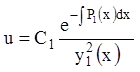 т.к.
т.к.
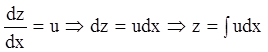 , т.к.
, т.к.
![]() , то
, то![]() .
.
Используем утверждение: если
известно одно ![]() ненулевое частное решение
линейного однородного уравнения (11.21), то порядок этого уравнения (11.21)
можно понизить на единицу, и второе частное решение находим по формуле:
ненулевое частное решение
линейного однородного уравнения (11.21), то порядок этого уравнения (11.21)
можно понизить на единицу, и второе частное решение находим по формуле:
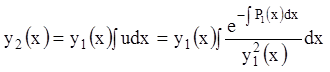 (положим
(положим
![]() ). (11.26)
). (11.26)
Тогда общее решение запишется:
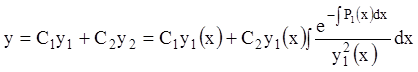 .
(11.27)
.
(11.27)
П р и м е р 1. Привести
уравнение цилиндрических функций (уравнение Бесселя) к каноническому виду: ![]() , или полагая
, или полагая ![]() :
:
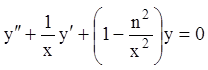 . (11.28)
. (11.28)
Условия теоремы существования
и единственности решения выполняются в интервалах ![]() ,
, ![]() – особая точка уравнения (11.28). Т.к.
– особая точка уравнения (11.28). Т.к.  , то
, то

и
уравнение Бесселя запишется ![]() , где
, где 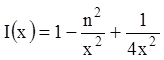 . Рассмотрим частный случай, выбрав
. Рассмотрим частный случай, выбрав 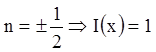 , и уравнение запишется
, и уравнение запишется ![]() . Откуда
. Откуда ![]() .
Учитывая, что
.
Учитывая, что ![]() и
и 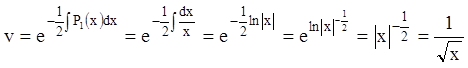 .
Тогда
.
Тогда 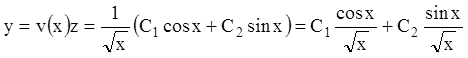 . Умножая частные решения
. Умножая частные решения 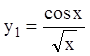 и
и  на
на ![]() , получим так называемые функции Бесселя:
, получим так называемые функции Бесселя:
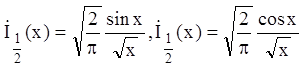 ,
,
тогда общее решение имеет вид:
 .
.
П р и м е р 2: Найти общее решение уравнения ![]() если
известно
если
известно 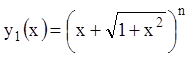 .
.
Р е ш е н и е. 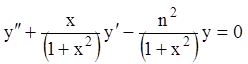 ,
,
 .
.
По формуле (11.26) 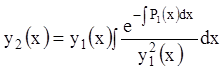
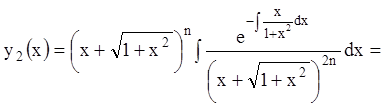
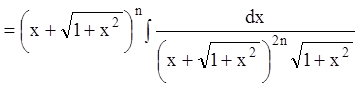 ;
;
замена: 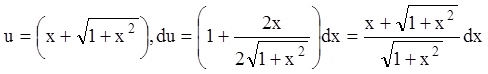 ,
,
тогда:
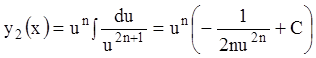 .
.
При ![]() частное
решение
частное
решение 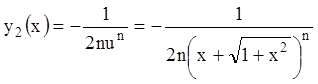 , а общее решение
, а общее решение 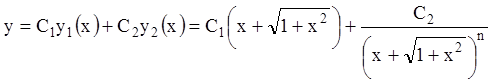 .
.
К каноническому виду можно
преобразовать уравнение (11.21) и путем замены независимой переменной.
Действительно, положим ![]() , тогда, если учесть
, тогда, если учесть
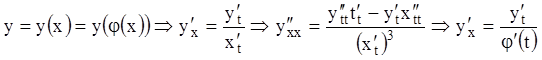 ;
;
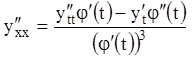 ,
,
уравнение ![]() запишется:
запишется:
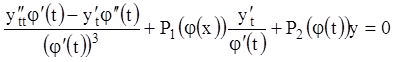
![]() или
или ![]()
![]() , или
, или 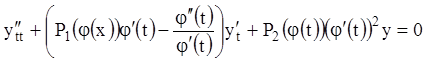 . Тогда из равенства
. Тогда из равенства 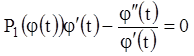 получим
получим 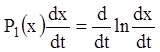 ;
;
(т.к.
 ). Тогда
). Тогда 
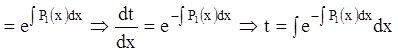 . Т.о. замена
. Т.о. замена ![]() приводит
уравнение (11.21) к каноническому виду:
приводит
уравнение (11.21) к каноническому виду:
![]() . (11.29)
. (11.29)
П р и м е р 3. ![]() .
.
Р е ш е н и е. Проведем
замену независимой переменной используя формулу ![]() . В
нашем случае
. В
нашем случае ![]() и
и ![]() ,
,
т.е. ![]() . Тогда
из уравнения (11.29) получаем
. Тогда
из уравнения (11.29) получаем 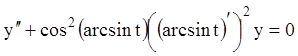 или
или
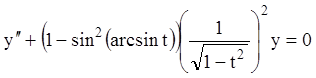 или
или 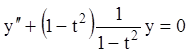 , или
, или ![]() ,
, ![]() ;
;
![]() .
.
Однородное линейное уравнение
2-го порядка, у которого коэффициент при ![]() равен
производной от коэффициента при
равен
производной от коэффициента при ![]() , т.е.
, т.е.
![]()
или
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.