Изучение явления переноса (примеры решения задач). Первое начало термодинамики, страница 8

АНАЛИЗ. В задаче рассматривается явление теплопроводности с точки зрения молекулярно-кинетической теории. Коэффициент теплопроводности рассчитывается по формуле . Этот коэффициент не зависит от давления при нормальных условиях. Зависимость проявляется, если давление настолько мало, что средняя длина свободного пробега молекулы  оказывается больше, чем расстояние между стенками сосуда, т. е.  > h. Следует найти минимальное давление, при котором проявляется зависимость .

РЕШЕНИЕ. Покажем, что при нормальных условиях коэффициент теплопроводности зависит от температуры и не зависит от давления. Воспользуемся для этого формулой .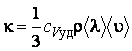

Учитывая, что

; ; ,

запишем

.

Если длина свободного пробега молекул больше расстояния между стенками сосуда h, то давление газа при таких условиях можно найти из формулы  > h.

Следовательно, минимальное значение давления p_min должно удовлетворять условию .

Проверим формулу на размерность: .

         Подставим численные значения:

.

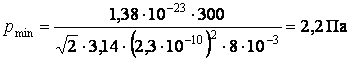Чтобы теплоемкость оказалась пониженной, давление остаточного газа между стенками дюаровского сосуда должно быть меньше 2,2 Па.

ОТВЕТ: p_min= 2,2 Па.

ЗАДАЧА 8. Найти показатель политропы n процесса, совершаемого идеальным газом при котором остается неизменным: а) коэффициент диффузии D, б) вязкость η, в) теплопроводность .

АНАЛИЗ. В задаче требуется, используя представления молекулярно-кинетической теории, найти показатель nполитропного процесса, при котором:

а) , б) ,
в) . Политропным называется процесс, при котором теплоемкость остается постоянной. Следует учесть, что уравнение политропы в различных переменных можно представить в виде: , ,

РЕШЕНИЕ. а) Запишем выражение для коэффициента диффузии как функцию давления p и температуры Т газа. Учтем, что , , тогда . Следовательно, .

По условию задачи D = const, т. е.  должна выполняться зависимость .

Запишем уравнение политропного процесса в виде , тогда , и , отсюда , n = 3.