Изучение явления переноса (примеры решения задач). Первое начало термодинамики, страница 10

.

Проверим формулу на размерность: .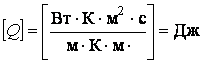

Подставим численные значения в формулу:

.

ОТВЕТ: Q = 23,7 кДж.

ЗАДАЧА 10. В однородном шаре, радиус которого R и теплопроводность , выделяется равномерно по объему тепловая мощность с объемной плотностью ω. Найти распределение температуры в шаре, если установившаяся температура на его поверхности T₀.

ДАНО: R  = const ω, Вт/м3 r = R T = T0

T(r) –?

АНАЛИЗ. Для решения задачи следует использовать закон Фурье, определяющий тепловой поток . Согласно условию задачи температура внутри шара изменяется, поэтому T = T(r). Тепловая мощность ω выделяется равномерно по объему с объемной плотностью ω и создает тепловой поток через поверхность сферы.

РЕШЕНИЕ. Внутри однородного шара выберем вспомогательную сферу радиуса r < R (рис. 1.2.5) и найдем тепловой поток через поверхность этой сферы (r < R): .

Получили дифференциальное уравнение. Для его решения проведем разделение переменных:
 . Проинтегрируем полученное выражение:

.             (1.2.15)

Воспользуемся начальными условиями и определим постоянную. Учтем, что при r = R
T = T₀, тогда имеем 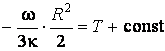, и .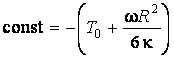

Подставим значение постоянной в уравнение (1.2.15). После математических преобразований найдем закон изменения температуры в зависимости от r:

.

Проверим формулу на размерность: .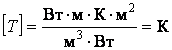

С увеличением расстояния r температура убывает, достигая минимального значения T_min = T₀ на поверхности шара. График функции T(r) представлен на рисунке 1.2.6.

ОТВЕТ: .

1.2.3. Задачи для самостоятельного решения

1.   Найти коэффициент диффузии водорода при нормальных условиях, если средняя длина свободного пробега молекул при этих условиях равна 1,6∙10^{–7 м. Построить график зависимости коэффициента диффузии водорода от температуры в интервале  при} p = 1,01∙10⁵ Па.

2.   При каком давлении отношение коэффициента внутреннего трения некоторого газа к коэффициенту его диффузии равно 0,3 г/л, а средняя квадратичная скорость его молекул равна 632 м/с?