Изучение явления переноса (примеры решения задач). Первое начало термодинамики, страница 4

С учётом обозначений, уравнение (1.2.1.) примет вид:         

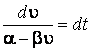.                                           (1.2.2)

После интегрирования выражения (1.2.2) и подстановки в него значений коэффициентов  и  получим закон изменения скорости со временем в виде:

.

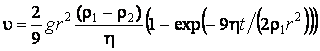Видно, что с ростом времени t скорость  приближается к максимальному значению                             

      ,                                      (1.2.3)

т.е. .

Функция  изображена на рис 1.2.3. Выражение для максимального  значения скорости  можно найти также из условия (1.2.1), приравняв  Таким образом, получим:  и в окончательном виде значение максимальной (предельной) скорости оказывается равной , что совпадает с выражением, полученным из закона (1.2.3).

Зависимость времени от скорости шарика найдем, интегрируя (1.2.2): 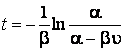. После подстановки коэффициентов α и β запишем функцию  в виде:

.

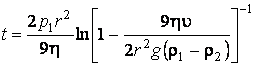Вычислим промежуток времени τ, через который скорость шарика станет равной :

.

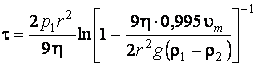Проверим формулу на размерность: .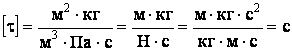

Найдем численное значение :

 м/с.

Подставим численные значения в формулу для определения промежутка времени τ:

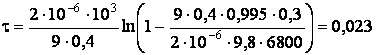 с.

Следовательно, спустя промежуток времени τ = 0,023 с для данной задачи расчеты коэффициента вязкости для жидкости можно вести по методу Стокса, считая скорость движения шарика постоянной.

ОТВЕТ: 0,023 с. 

ЗАДАЧА 4. Пространство между двумя коаксиальными цилиндрами А и В, заполнено водородом при температуре 27 ºС. Радиус внутреннего цилиндра равен  см, расстояние между цилиндрами  см. Внутренний цилиндр вращается, совершая 10 оборотов в секунду. Определить касательную силу f, действующую на   поверхности внешнего цилиндра В. Диаметр молекул водорода считать равным  см. Случай рассматривать как плоский.

ДАНО:	СИ