АНАЛИЗ. При решении задачи
следует воспользоваться уравнением теплового потока ![]() ,
учитывая, что коэффициент теплопроводности
,
учитывая, что коэффициент теплопроводности ![]() изменяется
с температурой по закону:
изменяется
с температурой по закону: ![]() (рис. 1.2.1),
где t – температура в градусах Цельсия.
(рис. 1.2.1),
где t – температура в градусах Цельсия.
|
Рис. 1.2.1 |
РЕШЕНИЕ. Запишем
уравнение Фурье в виде ![]() , где под dx
будем понимать бесконечно тонкий слой обмуровки, в пределах которого коэффициент
теплопроводности и температура t постоянны. Подставив значение
, где под dx
будем понимать бесконечно тонкий слой обмуровки, в пределах которого коэффициент
теплопроводности и температура t постоянны. Подставив значение ![]() , получим
, получим ![]() .
Разделим переменные этого дифференциального уравнения, а затем проинтегрируем:
.
Разделим переменные этого дифференциального уравнения, а затем проинтегрируем:
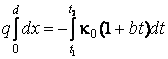 ,
,
следовательно, тепловой поток ![]() определится из равенства:
определится из равенства:
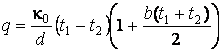 .
.
Проверим формулу на
размерность: 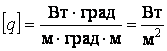 .
.
Подставим численные значения:
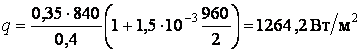 .
.
ОТВЕТ: ![]() .
.
ЗАДАЧА 3.При
определении вязкости жидкостей по методу Стокса расчёты ведут в предположении,
что скорость падения шарика постоянна и равна его скорости при установившемся
режиме движения: ![]() . В какой степени верно это
предположение? Через какой промежуток времени скорость шарика станет равной
. В какой степени верно это
предположение? Через какой промежуток времени скорость шарика станет равной ![]() , если плотность материала шарика
, если плотность материала шарика ![]() , его диаметр
, его диаметр ![]() ,
динамическая вязкость жидкости
,
динамическая вязкость жидкости ![]() ? В начальный
момент времени скорость шарика
? В начальный
момент времени скорость шарика ![]() .
.
|
ДАНО:
|
СИ
|
|
|
АНАЛИЗ. При решении задачи будем
использовать закон Стокса для расчёта силы сопротивления движению шарика в
жидкости: ![]() , где r – радиус шарика,
, где r – радиус шарика, ![]() – вязкость жидкости,
– вязкость жидкости, ![]() – скорость шарика.
– скорость шарика.
РЕШЕНИЕ. Составим
дифференциальное уравнение движения шарика массы m: ![]() . В проекции на ось OY (рис
1.2.2.) получим:
. В проекции на ось OY (рис
1.2.2.) получим:
![]() ,
(1.2.1.)
,
(1.2.1.)
где r2 – плотность жидкости.
|
Рис. 1.2.2 |
Решим дифференциальное уравнение
(1.2.1) методом разделения переменных и найдём время t, по истечении
которого скорость шарика станет равной некоторому значению ![]() . Для этого обозначим величину
. Для этого обозначим величину ![]() , коэффициент перед переменной
, коэффициент перед переменной ![]() через
через ![]() .
Учтём, что
.
Учтём, что ![]() , где
, где ![]() –
объём шарика. Следовательно,
–
объём шарика. Следовательно,![]() , а
, а 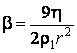 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.