Изучение явления переноса (примеры решения задач). Первое начало термодинамики, страница 5

АНАЛИЗ. При решении задачи следует рассматривать возникающие в газе при движении цилиндра А силы внутреннего трения F, направленные по касательной к слоям газа. В результате между слоями газа действует сила . Скорость газа у поверхности твёрдого тела совпадает со скоростью самой поверхности. Таким образом, на поверхность S цилиндра В действует такая же по величине сила F. На единицу поверхности цилиндра действует сила , а на поверхность  – сила . Коэффициент внутреннего трения определяется согласно молекулярно-кинетической теории по формуле . 

РЕШЕНИЕ. Найдём градиент скорости , где  –  скорость течения слоёв газа, причём   –  скорость газа у поверхности внутреннего цилиндра,   –  скорость газа у поверхности внешнего цилиндра В. Скорости  и  равны скоростям самих поверхностей А и В. Их значения можно найти, зная угловую скорость цилиндров. Таким образом, , , поэтому

.

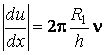Проверим формулу на размерность: .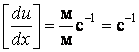

Подставим численные значения: .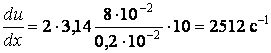

Определим коэффициент внутреннего трения по формуле:

.                                                 (1.2.5)

Среднюю  арифметическую скорость теплового движения молекул и среднюю длину  свободного пути найдём по формулам, рассчитанным в молекулярно-кинетической теории:

; .

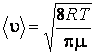Плотность  водорода при заданной температуре Т получим из уравнения состояния идеального газа: 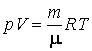. Таким образом, . Давление  связано с числом молекул n в единице объёма уравнением: , т. е.  . Подставим значения ,, и n в формулу для коэффициента вязкости (1.2.5). В результате запишем:

.

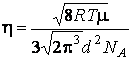Проверим размерность формулы:

.

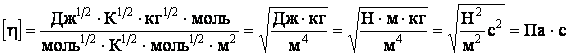Подставим численные значения, найдём вязкость водорода в данных условиях:         

.

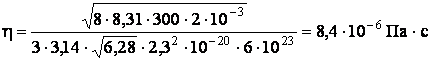Воспользовавшись численными значениями для градиента скорости (1.2.4) и динамической вязкости , определим силу, действующую на площадку , внешнего цилиндра B, по формуле:

.