Изучение явления переноса (примеры решения задач). Первое начало термодинамики, страница 6

Проверим формулу на размерность: .

Подставим численные значения: .

Сила, действующая на внешний цилиндр, заставляет его поворачиваться в том же направлении, в котором вращается внутренний цилиндр.

ОТВЕТ: .

ЗАДАЧА 5. Найти количество азота, прошедшего вследствие диффузии через площадку 100 см² за 10 с, если градиент плотности в направлении, перпендикулярном к площадке, равен . Температура азота 27 ºС, средняя длина свободного пробега молекул азота  см.

ДАНО:	СИ

АНАЛИЗ. При решении задачи следует воспользоваться законом Фика, определяющим массу газа, перенесённого при диффузии за время  через площадку :

.           (1.2.6)

Коэффициент диффузии согласно расчётам молекулярно-кинетической теории определяется формулой:

.                    (1.2.7)

Средняя арифметическая скорость теплового движения молекул рассчитывается по формуле:

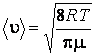 .                                             (1.2.8)

РЕШЕНИЕ. Подставим значение коэффициента диффузии из формулы (1.2.7) в закон Фика (1.2.6), получим:

.

Учтём формулу (1.2.8) и запишем окончательное выражение для массы газа, переносимого через площадку  за время  за счёт его диффузии:

.

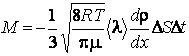Проверим формулу на размерность:

.

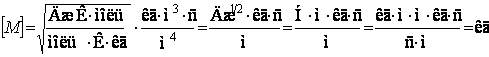Подставим численные значения:

.

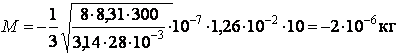Знак «–» указывает на то, что вещество переносится в направлении убывания концентрации газа.

ОТВЕТ: .

ЗАДАЧА 6. Как изменится коэффициент диффузии  и вязкость  идеального газа, если его объём увеличить в n раз: а) изотермически; б) изобарно. (см. рис. 1.2.4)

ДАНО:

АНАЛИЗ. В задаче требуется показать, как изменяются коэффициент диффузии D и вязкость  идеального газа при изменении его объёма: а) при  , б) при . Для анализа следует использовать формулы для коэффициентов диффузии и вязкости, полученные в молекулярно-кинетической теории: ; , а так же уравнения изотермического и изобарного процессов.