Дискретные цикловые системы автоматического управления: Методические указания к выполнению лабораторных работ по курсу «Автоматизация производственных процессов в машиностроении», страница 7

       Минимизированное выражение функции может быть получено при использовании специальной таблицы, называемой картой Карно. Каждой клетке этой таблицы ставится в соответствие определенная конъюнкция переменных, причем делается это таким образом, чтобы соседние конъюнкции отличались лишь значениям одного из сомножителей. Например, для функции 3-х переменных комбинации их значений можно записать в виде ряда из следующих конъюнкций, каждая из которых отличается только одним сомножителем:

, , , , , , , .

       Карта Карно для рассмотренной выше функции может быть представлена в виде табл. 7а или 7б.

       При заполнении таблицы в каждую клетку заносят значение функции , которое она имеет при соответствующей комбинации значений переменных. Например, в клетку, отмеченную дизъюнкцией , ставят 1, так как при значении переменных , ,  согласно таблице истинности . В клетку  ставят 0, так как в таблице истинности для набора значений переменных (, , ) . В клетки, соответствующие неиспользованным состояниям, можно ставить те значения функции, которые позволяют получить наиболее простое ее выражение. Таким образом, заполняют все клетки таблицы. Затем контурами в виде прямоугольников выделяют зоны рядом расположенных единиц. Число единиц в контуре должно быть целой степенью числа 2.

       Таблица 3.7 – Карты Карно

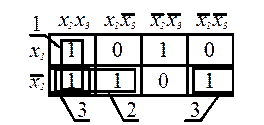
       Для записи уравнения функции для каждого контура записывают новое выражение дизъюнкции, которое получается путем вычеркивания переменных, изменяющих свое значение в пределах данного контура (зоны). В карте Карно (табл. 7б) выделено 3 контура, для которых записывают следующие конъюнкции: 1) ; 2) ; 3) . Затем записывают выражение функции как сумму полученных конъюнкций и конъюнкций для отдельных клеток, обозначенных "логической 1". Таким образом, выражение функции будет

.

       Электрическая схема, соответствующая этой функции, приведена на рис. 5.

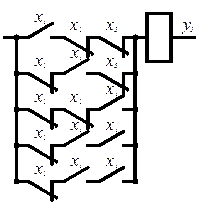
       Рисунок 5 – Схема полученная с использованием карты Карно

       Для функции 4-х переменных  возможное количество комбинаций значений переменных . Пусть, например, функция  задана таблицей истинности (табл. 8).

       Таблица 3.8 – Таблица истинности функции

	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
	0	1	0	0	1	1	0	1	0	1	0	0	0	1	1	0

       Карта Карно, построенная по данным таблицы 8, приведена в виде табл. 9.

       Таблица 3.9 – Карта Карно для функции

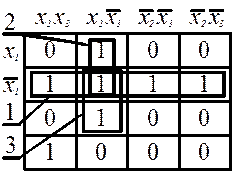
       В карте выделено 3 зоны рядом стоящих единиц, и осталась одна клетка, содержащая единицу. Записывая уравнение как сумму дизъюнкции зон и одиночных клеток, содержащих единицу, получаем

.

       Этой функции соответствует схема (рис. 6).

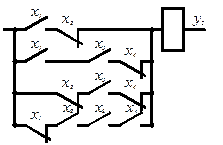
       Рисунок 6 – Схема, реализующая функцию

       Полученное на основе использования алгебры логики аналитическое выражение функции является одной из форм записи алгоритма управления. Так как при автоматизации объекта возникает необходимость управления рядом исполнительных механизмов, то алгоритм управления может быть представлен в виде системы логических уравнений.