Дискретные цикловые системы автоматического управления: Методические указания к выполнению лабораторных работ по курсу «Автоматизация производственных процессов в машиностроении», страница 5

       Логические функции могут быть реализованы с использованием релейно-контактных схем. В этих схемах для реализации каждой функции предусматривают отдельную электрическую цепь, которая содержит управляющие, контакты и исполнительный элемент, называе­мой нагрузкой. В роли нагрузки выступают лампы накаливания катушки реле, пускателей магнитов и т.п. При формальном представлении схем в виде логических функций воздействия на контакты рассматриваемой цепи отождествляют с логической переменной, ко­торая имеет два значения: 0 – нет воздействия, 1 – есть воздействие. Напряжение на нагрузке представляют как логическую функцию, которая может иметь два значения: 0 – нет напряжения, 1 – есть напряжение. Рассмотрим простейшую электрическую цепь, пред­ставляющую собой последовательное соединение кнопки, имеющей замыкающий контакт, и лампы накаливания (рис. 1а).

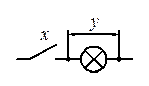
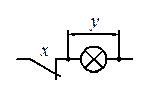
       Рисунок 1 – Примеры простейших электрических цепей

       Если кнопка не нажата (нет воздействия, ) – лампа не горит (нет напряжения, ). Если кнопка нажата (есть воздействие, ) – лампа горит (есть напряжение, ). Состояние лампы и состояние кнопки связаны зависимостью .

       Электрическая цепь, представляющая собой последовательное соединение кнопки, имеющей размыкающий контакт, и лампы накаливания (рис. 1б), обеспечивает связь между состоянием лампы и кнопки в соответствии с формулой , т.е. если нет воздействия на кнопку (), есть напряжение на лампе (), если есть воздействие на кнопку (), то нет напряжения на лампе ().

       Таким образом, кнопка с замыкающим контактом в рассматриваемой схеме реализует функцию повторения, а кнопка с размыкающим контактом реализует функцию отрицания. При записи логических функций способ воздействия на контакты (вручную, механически от кулачков, упоров или от электромагнитов) является несущественным и на вид уравнений не влияет. Существенным является лишь исполнение контакта. В аналитическом выражении функции замыкающему контакту соответствует переменная без знака инверсии, а размыкающему – со знаком инверсии (табл. 2).

       В общем случае функция  переменных может быть реализована в виде цепи, в которой управление напряжением на нагрузке будет осуществляться путем соответствующего соединения  контактов. Причем, как это видно из табл. 3, операции логического умножения переменных в выражении функции соответствует последовательное соединение контактов на схеме, а операции логического сложения – параллельное соединение.

       Используя это соотношение, можно по выражению функции получить релейно-контактную схему для ее реализации, а по имеющейся схеме найти аналитическое выражение функции.

       Для того, чтобы перейти от аналитического выражения функции к релейно-контактной схеме, необходимо:

Ø  каждой переменной, входящей в выражение функции, поставить в соответствие контакт, причем для переменной, не имеющей знака инверсии – контакт замыкающий, а имеющей знак инверсии – контакт размыкающий;

Ø  соединить контакты (или группы контактов) последовательно или параллельно в зависимости от действий (умножение или сложение), выполняемых над соответствующими переменными в выражении функции;

Ø  последовательно полученной совокупности контактов подсоединить нагрузку (т.е. изобразить элемент, отождествляющий функцию).

       Например, функцию  можно реализовать с использованием схемы (рис. 2а).

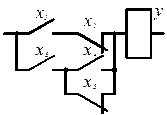
       Рисунок 2 (а, б) – Релейно-контактные схемы для реализации функций:

       а) ;      б) 

       Для получения выражения функции по заданной релейно-контактной схеме необходимо:

Ø  каждому замыкающему контакту поставить в соответствие переменную без знака инверсии, а размыкающему – со знаком инверсии;

Ø  записать формулу, отражая последовательное соединение контактов как логическое умножение, а параллельное соединение – как логическое сложение.