Дискретные цикловые системы автоматического управления: Методические указания к выполнению лабораторных работ по курсу «Автоматизация производственных процессов в машиностроении», страница 6

       Действуя таким образом, для схемы, изображенной на рис. 2б, получаем аналитическое выражение функции .

       Для реализации логических функций используют и бесконтактные электронные устройства, которые принято называть логическими элементами. Условное обозначение наиболее распространенных элементов приведено в табл. 2 и 3.

       В качестве примера на рис. 3 изображена электрическая схема с логическими элементам. Схема реализует функцию  релейно-контактная схема, для которой была приведена на рис. 2а.

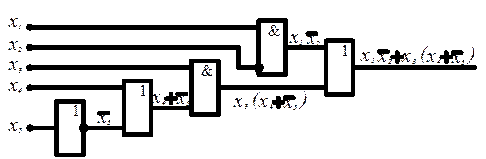
       Рисунок 3 – Электрическая схема с условным обозначением логических элементов и записью выполняемых ими преобразований сигналов

       Комбинационной называют схему, в которой выходные переменные однозначно зависят от комбинаций значений входных переменных; комбинационная схема не содержит элементов памяти.

       Закон функционирования комбинационной схемы может быть задан в виде таблицы истинности или в виде формулы.

       Существуют два способа составления логической формулы по известной таблице истинности.

       По первому способу находят в таблице все наборы значения аргументов, при которых функция принимает значение 1, и для каждого набора записывают конъюнкции (произведение) аргументов. В соответствующее произведение вписывают , если значение этого аргумента равно 1 в данном наборе, и  (инверсию), если аргумент равен 0. Все полученные конъюнкции объединяют знаками дизъюнкции (суммируют). Такая форма записи логической функции называется совершенной дизъюнктивной нормальной формой (СДНФ). При использовании совершенной дизъюнктивной нормальной формы записи функция (СДНФ) вообще отпадает необходимость в заполнении таблицы истинности, так как при этой форме записи используют только значения функции равные 1.

       По второму способу записывают сначала дизъюнкции (суммы) аргументов для тех наборов, где функция принимает значение 0. При этом вписывают , если значение аргумента в соответствующем наборе равно 0, и , если аргумент равен 1. Затем все полученные суммы объединяют знаками конъюнкция: (перемножают). Данная форма записи функции называется совершенной конъюнктивной нормальной формой (СКНФ).

       Например, для функции, заданной таблицей истинности (табл. 6), можно получить следующие два варианта формул:

; (СДНФ)
, (СКНФ)
каждая из этих формул может быть реализована в виде релейно-контактной схемы. На рис. 4 приведены соответствующие этим формулам схемы.

       Таблица 3.6 – Таблица истинности искомой функции

	0	1	0	1	0	1	0	1
	0	0	1	1	0	0	1	1
	0	0	0	0	1	1	1	1
	0	1	1	0	1	0	1	1

      

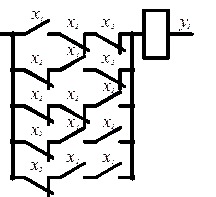
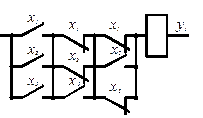
       Рис.4. Схемы для двух форм записи функций:

       а) для СДНФ; б) для СКНФ

       Схема, соответствующая первой форме записи уравнения – (СДНФ), является более удобной. В ней каждая цепь контактов обеспечивает подключение нагрузки на соответствующих этапах цикла. В данном примере вторая форма записи уравнения (СКНФ) позволяет получить схему (рис. 4б), имеющую общее число контактов меньше, чем в первой схеме. Это связано с тем, что в данном случае число состояний в таблице истинности, обеспечивающих "логический 0" функции, меньше, чем число состояний, обеспечивающих "логическую 1".

       Путем алгебраических преобразований можно упростить выражение полученных функций – минимизировать их, т.е. уменьшить число контактов в схеме, реализующей функцию.