Прямая линия на плоскости

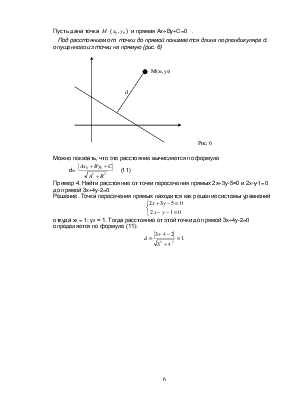
Фридман М.Н.

Лекция на тему:

ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ

            Определение. Углом  наклона  прямой к оси ОХ называется минимальный угол, на который надо повернуть  прямую  против часовой стрелки до совмещения с осью ОХ.

                                                       Рис 1.

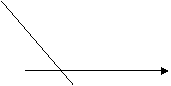
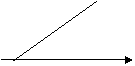
Как видно из  рис.1, это может быть острый (1.1), тупой (1.2) или прямой (1.3) угол, а также   =0  (1.4).

         Определение. Угловым  коэффициентом k прямой  называется тангенс угла наклона прямой к оси X, (если он существует): .

         Очевидно, что для прямой , образующей острый угол с осью OX,  (1.1); для прямой, образующей тупой угол с осью OX, ;если прямая параллельна оси OX, то  (1.4); а для прямых, перпендикулярных оси OX, угловой коэффициент не существует (1.3).

         Определение. Уравнением линии L на плоскости называется уравнение вида:  (1) такое, что координаты любой точки линии, и только они, удовлетворяют этому уравнению.

             Например, уравнение окружности радиуса R с центром в начале координат имеет вид: .

            Однако не всякое уравнение вида 1 задает линию на плоскости. Так, например, уравнение  задает не линию, а точку – начало координат, а уравнение  вообще не имеет геометрического образа на действительной плоскости!

              Темой данной лекции является уравнение прямой на плоскости, его виды и анализ.

             1. Уравнение прямой с угловым коэффициентом.

       Пусть на плоскости задана прямая  с угловым коэффициентом k , пересекающая ось OY в точке B (0;b) (см. рис 2).