Несобственные интегралы с бесконечными пределами интегрирования
Пусть функция ![]() определена для всех
определена для всех ![]() и интегрируема в любом отрезке
и интегрируема в любом отрезке
![]() . Если существует
. Если существует
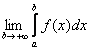
то этот предел
называется несобственным интегралом функции ![]() на
промежутке
на
промежутке ![]() и обозначается
и обозначается 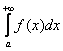 . В этом случае говорят также, что
несобственный интеграл
. В этом случае говорят также, что
несобственный интеграл 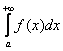 сходится, а
функция
сходится, а
функция ![]() интегрируема в несобственном смысле
на промежутке
интегрируема в несобственном смысле
на промежутке ![]() . В противном случае
говорят, что интеграл
. В противном случае
говорят, что интеграл 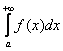 расходится, а
функция
расходится, а
функция![]() неинтегрируема в несобственном
смысле на промежутке
неинтегрируема в несобственном
смысле на промежутке ![]() .
.
Для непрерывной
неотрицательной функции ![]() ,
, ![]() , сходящийся несобственный интеграл
, сходящийся несобственный интеграл 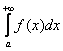 равен площади неограниченной
криволинейной трапеции
равен площади неограниченной
криволинейной трапеции ![]() .
.
Аналогично определяется
несобственный интеграл функции ![]() ,
, ![]() , с нижним бесконечным пределом
интегрирования:
, с нижним бесконечным пределом
интегрирования:

Несобственный интеграл с
бесконечными верхним и нижним пределами интегрирования функции ![]() ,
, ![]() ,
определяется следующим образом:
,
определяется следующим образом:
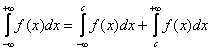
где c – некоторое число.
Если для функции ![]() ,
, ![]() ,
при некотором
,
при некотором ![]() существуют интегралы
существуют интегралы
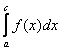
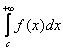
то 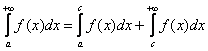
Если хотя бы один из интегралов в
правой части этого равенства не существует, то интеграл 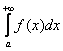 называется
расходящимся.
называется
расходящимся.
Признак сходимости и расходимости интегралов для неотрицательных функций (признаки сравнения). Пусть функции f(x) и g(x) неотрицательны и интегрируемы на любом отрезке [a; b], b<+∞. Тогда:
I. Если f(x) и g(x) удовлетворяют на промежутке [a; +∞) неравенству f(x)≤g(x), то:
a) из
сходимости интеграла 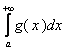 следует сходимость
интеграла
следует сходимость
интеграла 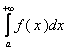 ;
;
b) из
расходимости интеграла 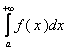 следует
расходимость интеграла
следует
расходимость интеграла 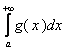 .
.
II. a) Если g(x)>0 на промежутке [a; +∞) и существует
![]()
То, если 0≤k<+∞, то из
сходимости 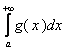 следует сходимость интеграла
следует сходимость интеграла 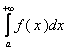 .
.
Если 0<k≤+∞, то из расходимости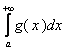 следует расходимость интеграла
следует расходимость интеграла 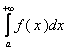 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.