Следствие: Если f(x)~g(x) при ![]() , то f и g одновременно либо интегрируемы, либо неинтегрируемы на
промежутке [a; +∞).
, то f и g одновременно либо интегрируемы, либо неинтегрируемы на
промежутке [a; +∞).
Основные формулы для несобственных интегралов на бесконечном промежутке.
1. Линейность интеграла. Если несобственные интегралы
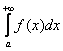
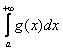 сходятся, то для любых чисел p и q сходится интеграл
сходятся, то для любых чисел p и q сходится интеграл
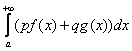
причем
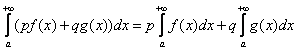
2. Формула Ньютона—Лейбница. Если
функция ![]() ,
, ![]() ,
непрерывна и
,
непрерывна и ![]() ,
, ![]() ,
— какая-либо ее первообразная, то
,
— какая-либо ее первообразная, то
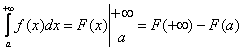
где ![]()
3. Формула замены переменной.
Пусть ![]() ,
, ![]() —
не прерывная
—
не прерывная ![]() ,
,![]() ,
,![]() — непрерывно дифференцируемая
функции, причем
— непрерывно дифференцируемая
функции, причем
![]()
тогда
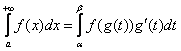 (2)
(2)
Формула (2) справедлива в случае сходимости по крайней мере
одного из двух входящих в нее интегралов. В случае расходимости
одного из интегралов расходится и другой.
4. Формула интегрирования по
частям. Если ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
— непрерывно дифференцируемые функции и
,
— непрерывно дифференцируемые функции и ![]() существует,
то
существует,
то
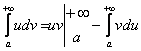 (3)
(3)
где
![]()
Формула (3) справедлива в случае сходимости по крайней мере одного из двух входящих в нее интегралов. В случае расходимости одного из интегралов расходится и другой.
N102
![]()
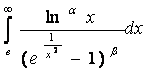
![]()
![]() при
при ![]()
![]()
Откуда 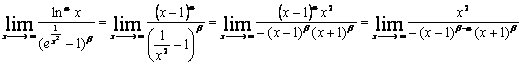
![]()
Откуда ![]() . При этом условии
интеграл сходится.
. При этом условии
интеграл сходится.
N103
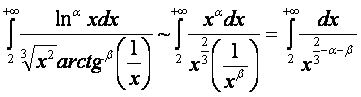

При![]() интеграл
сходится
интеграл
сходится ![]()
N104
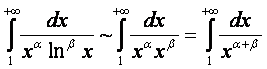
![]()
![]() - интеграл сходится
- интеграл сходится
N105
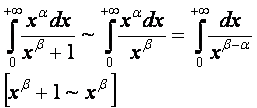
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.