Прямая линия на плоскости, страница 3

Вычитая это уравнение из уравнения 2, получаем:

   (4) -уравнение прямой ,проходящей  через данную точку в данном направлении.

Пример1.

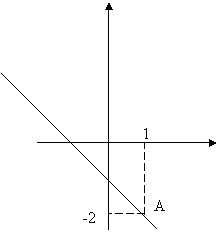
Составить уравнение прямой, проходящей через точку A(1, -2):

а) под углом  к оси ОХ:

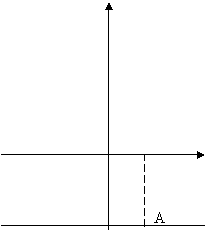
б) параллельно оси ОХ;

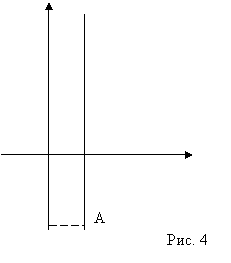
в) перпендикулярно оси ОХ.

Решение. а)  Используем уравнение( 4), где , получаем:

, или .

б) В этом случае k=0, уравнение имеет вид:.

в) В этом случае угловой коэффициент не существует, уравнение имеет вид (3), т.е. .

 

3. Уравнение прямой ,проходящей  через две  данные  точки.

Пусть прямая проходит через две точки с попарно различными координатами:

 и , где  и .

 Очевидно, что в этом случае ее угловой коэффициент существует : (5).

Тогда  , применяя уравнение (4)  например, к точке , лежащей на прямой, получаем:  (6) -уравнение прямой ,проходящей  через две  данные  точки.

Пример2.

Составить уравнения прямых , проходящих через точки :

а) А (2, 3 ) и В (5,6);

б) А (2,3) и  С (-1,3)..

Решение. а) По  формуле (6) получаем: y-3=1(x-2), или y=x+1.

б) Формула (6) в данном случае неприменима, т.к. Уравнение этой прямой: y=3.

4.  Общее уравнение прямой и его исследование.

Рассмотрим уравнение вида

Ax+By+C=0 (7), где А и В одновременно в нуль не обращаются.

Покажем, что это уравнение описывает все виды прямых на плоскости.

1.Пусть В0, тогда уравнение можно записать в виде:.т.е. получено уравнение прямой с угловым коэффициентом  у=kx+b, где   , .

Если С=0, то прямая проходит через начало координат, если А=0, то прямая параллельна оси ОХ, если и А=0, и С=0, то прямая совпадает с осью ОХ.

2.Пусть В=0, тогда,  по условию, А0.Разделив уравнение (7) на А, получаем:

, т. е. уравнение прямой, перпендикулярной  оси OX:  х=a, где а=.