5. Точка пересечения прямых. Расстояние от точки до прямой.
Пусть даны
две прямые ![]() и
и ![]() .
.
Координаты точки их пересечения удовлетворяют каждому из уравнений,
то есть являются решением системы уравнений:
![]()
![]()
Если прямые не параллельны, то решение системы определяет единственную точку пересечения прямых.
Пусть дана
точка ![]() (
(![]() )
и прямая Ax+By+C=0 .
)
и прямая Ax+By+C=0 .
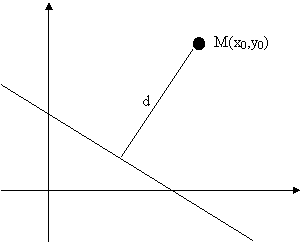
![]() Под расстоянием от точки до прямой
понимается длинa перпендикуляра d,
Под расстоянием от точки до прямой
понимается длинa перпендикуляра d,
опущенного из точки на прямую (рис. 6)
 |
|||
|
|||
Можно показать, что это расстояние вычисляется по формуле
d= 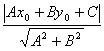 (11)
(11)![]()
Пример 4. Найти расстояние от точки пересечения прямых 2x+3y-5=0 и 2x-y-1=0 до прямой 3x+4y-2=0.
Решение. Точка пересечения прямых находится как решение системы уравнений
![]()
откуда x0 = 1; y0 = 1. Тогда расстояние от этой точки до прямой 3x+4y-2=0 определяется по формуле (11):
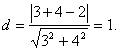
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.