Прямая линия на плоскости, страница 4

В частном случае, при С=0, получаем х=0  -  уравнение оси ОУ.

Таким образом, мы показали, что уравнение (7)  описывает все виды прямых на плоскости.

Уравнение Ax+By+C=0   (7), где А и В одновременно в нуль не обращаются, называется общим уравнением прямой на плоскости.

5.Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых.

Пусть даны две прямые с угловыми коэффициентами:

 и .

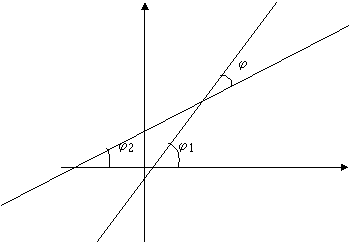
Для определенности будем рассматривать острый угол  между ними .

			Рис. 5

 

      Из рис.5 видно, что 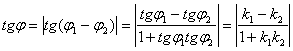 (8).

      Из этой формулы вытекает, что:

1. Прямые параллельны тогда и только тогда, когда числитель в формуле (8) равен нулю, т.е.  = (9), угловые коэффициенты прямых равны.. В частном случае, когда и  , прямые совпадают.
2. . Прямые перпендикулярны  тогда и только тогда, когда  знаменатель в формуле (8) равен нулю, откуда  (10) т.е. угловые коэффициенты противоположны по знаку и обратны по величине.

Пример3..

Составить уравнения прямых , проходящих через точку А (5,1) параллельно и перпендикулярно прямой .

Решение.

Угловой коэффициент исходной прямой равен= .

Угловой коэффициент параллельной прямой совпадает с , а для перпендикулярной прямой по формуле (10)  он равен  . Применяя формулу (4), получаем уравнения:

параллельной прямой y-1=(x-5), т.е  y=x+3; или 2х+5у-15=0.

перпендикулярной прямой y-1=(x-5), т.е  y= x-. Или 5х-2у-23=0.

    Условия параллельности и перпендикулярности для прямых, заданных общими уравнениями  и , с угловыми коэффициентами  и  , где  и , могут быть записаны следующим образом:

Параллельности:.

Перпендикулярности: .