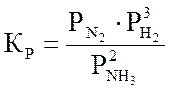Лабораторный практикум по дисциплинам "Технология и оборудование отрасли" и "Макрокинетика и расчет реакторов", страница 13

                    ,                                                                (3.2)

где К_Р- константа равновесия реакции;    - парциальные давления аммиака, азота и водорода в равновесной смеси.

          Парциальные  давления можно выразить через давление смеси и объемную концентрацию  компонента.  Обозначив, соответственно, равновесные концентрации аммиака, азота и водорода, об. %, и Р –  давление смеси. В этом случае:

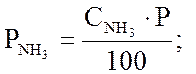
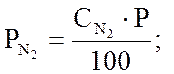
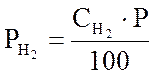                                     (3.3)

уравнение (3.2) примет вид:

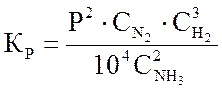                                                 (3.4)

          Для решения уравнения (3.4) воспользуемся дополнительными уравнениями:

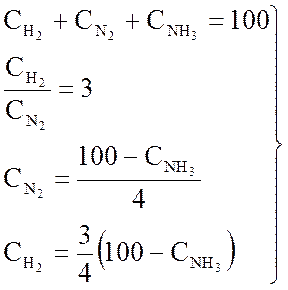                                                          (3.5)

          Подставив последние выражения в уравнение  (3.4) получим  уравнение равновесия

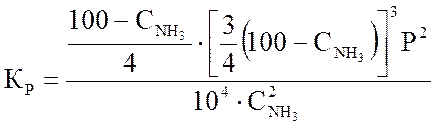                                           (3.6)

Проведя преобразования, получим квадратное уравнение

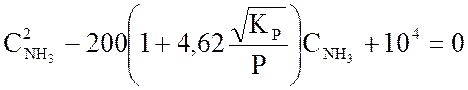                                     (3.7)

          Константу равновесия вычисляем из эмпирического уравнения А.Т. Ларсона и Р.Л. Доджа

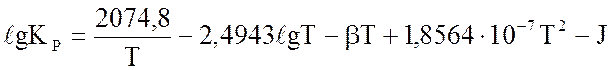          ,           (3.8)

где β – коэффициент, зависящий от давления, J – константа интегрирования.

Значения β и J в зависимости от давления представлены в  таблице 3.1.

          По уравнению (3.7) с использованием уравнения (3.8) рассчитываем равновесные концентрации аммиака при различных давлениях и температурах.*

----------------------------------------------------------------------------------------------------* Предложенный метод расчета приближенный. Для точного расчета в уравнение для константы равновесия следует подставлять не парциальные давления компонентов, а парциальные летучести, определение которых является весьма трудной задачей.

                                                                                                    Таблица 3.1.

                   Значения β и J при различных давлениях

Давление,   МПа	β	J	Давление,  МПа	β	J
1	0	-1,933	30	1,256∙10-4	-2,206
3	3,4∙10-5	-2,021	60	1,0856∙10-3	-3,059
5	1,256∙10-4	-2,090	100	2,6833∙10-3	-4,473
10	1,256∙10-4	-2,113

          Уравнение (3.7) предполагает, что в исходной реакционной смеси содержатся только азот и водород и отсутствуют инертные примеси. Равновесную концентрацию аммиака в присутствии инертов можно пересчитать с использованием следующего выражения:

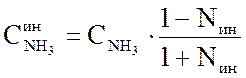                                                          (3.9)

Цель работы

Изучить влияние температуры   давления и содержания инертных примесей   на равновесную концентрацию аммиака в реакционной смеси. Представить полученные результаты  в виде графиков и объяснить их и сделать соответствующие выводы.

Порядок выполнения работы

Запустить имитатор  лабораторной работы.

     Имитатор к лабораторной работе позволяет при различных температурах, давлениях и разном содержании инертных примесей в исходной азотоводородной смеси   равновесное содержание аммиака в газе. 

Пользуясь описанием имитатора  к лабораторным работам, (см. приложение) установить, согласно заданию, интервал и шаг изменения  температуры на термометре, давление и содержание инертных примесей. После того как все параметры будут установлены, следует нажать кнопку «расчет».  В ходе работы можно менять содержание инертов и давление.

          Варианты заданий приведены в таблице 3.2.

          Полученные расчетные значения равновесных  концентраций аммиака заносим в таблицу расчетных величин. Примерный вид таблицы показан ниже: таблица 3.3.

          На основании данных, представленных в таблице 3.3. строятся графические зависимости:

          - равновесной концентрации аммиака от температуры при различных  давлениях и постоянном содержании инертов;

                                                                                                          Таблица 3.2.