Распространение земных радиоволн, страница 9

Зоны Френеля. Область пространства, существенно участвующая в распространении радиоволн.  Геометрическая (лучевая) трактовка механизма распространения радиоволн не отражает тот факт, что в действительности волна из пункта А в пункт В распространяется не по тоненькой ниточке – “лучу” АВ, а в пределах определенного объема пространства вокруг оси АВ. Аналогично можно судить и об определенной области на поверхности Земли, в пределах которой формируется зеркально отраженный луч. Оба эти вопроса решаются на основании принципа Гюйгенса и понятия зон Френеля.

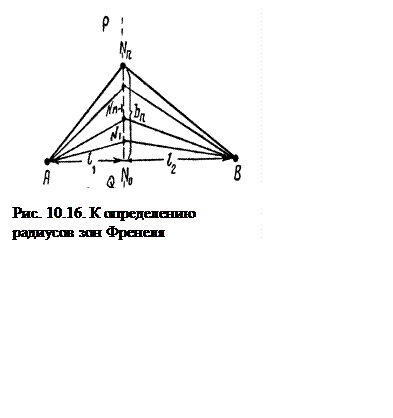
Пусть в пункте А (рис. 10.16.) находится изотропный источник излучения радиоволн. В соответствии с принципом Гюйгенса в пункте В результирующее поле является суммой полей вторичных источников, расположенных на фронте волны. Для простоты представим фронт сфе-рической волны в виде плоскости PQ. Проведем из точки В семейство прямых, пересекающих плоскость PQ в точках, удаленных от точки В на расстояние 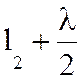. Это семейство образует коническую поверхность. Образующей конической поверхности являются прямая ВN₁. Аналогично строятся конические поверхности высших порядков, для которых 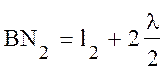 и вообще  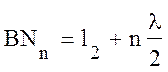. Пересечение конических поверхностей с плоскостью PQ образует систему концентрических окружностей. Вид на эти окружности на сферическом фронте со стороны точки В показан на рис. 10.17. Участки, заключенные между соседними окружностями получили название зон Френеля (по имени французского физика Френеля, внесшего большой вклад в оптику). Первая зона Френеля представляет собой круг на фронте волны, а зоны высших порядков представляют собой кольцевые области.

Воображаемые вторичные источники излучения, расположенные в пределах первой зоны Френеля, характеризуются тем, что фазы колебаний, создаваемых ими в точке В, отличаются от фазы колебаний, создаваемых вторичным источником в точке N₀, не более чем на π ().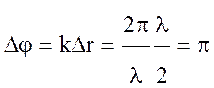

Фазы колебаний, создаваемых вторичными источниками излучения, расположенными в пределах 2-й зоны Френеля, отличаются от фазы колебаний источника N₀ на величину от π до 2π. Можно сказать, что в целом колебания, создаваемые 2-й зоной, отличаются по фазе от колебаний, создаваемых 1-й зоной, на π и т.д. На рис. 10.17. фазы колебаний отмечаются условно плюсами и минусами.

Если в точке В сложить поля, создаваемые всеми зонами Френеля, то получим следующее выражение:

Е = Е₁ – Е₂ + Е₃ – Е₄ + Е₅ – Е₆ + … .                                            (10.46)

Учитывая, что всегда kr>>1, можно сделать вывод, что поля соседних зон взаимно частично компенсируются, и последнее выражение можно записать в следующем виде:

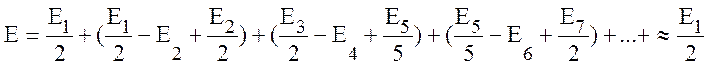.           (10.47)