Распространение земных радиоволн, страница 7

Во многих случаях формула (10.32) может быть подвергнута дальнейшему упрощению. Если с ростом расстояния аргумент синуса становится равным, или меньшим 20⁰, то синус может быть заменен его аргументом, и формула (10.32) примет вид:

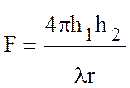                                 .                                       (10.38)

Подставляя это значение в формулу (10.4) с учетом (10.6) и переходя к более удобной для расчетов форме, получим:

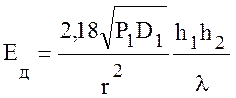            ,   ,                           (10.39)

где   Р₁ – в кВт,  h₁ h₂ – в м,  l - в м,   r – в км.

Формула (10.39) была получена в 1928 г. Б.А. Введенским и называется квадратичной формулой Введенского. «Квадратичный» характер формулы состоит в том, что в отличие от свободного пространства, в данном случае напряженность поля убывает обратно пропорционально квадрату расстоянию. Область применимости формулы Введенского можно определить из условия :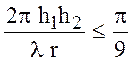

,

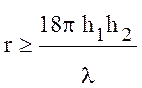что в четыре с половиной раза превышает расстояние до последнего максимума.

Учет кривизны Земли. При значительных расстояниях от передатчика при использовании интерференционных формул необходимо учитывать кривизну Земли. Кривизна Земли ограничивает дальность радиосвязи прямыми лучами при заданных высотах передающей и приемной антенн.

Максимальное расстояние для радиосвязи прямым лучом называется расстоянием прямой видимости. На рис. 10.10. расстояние прямой видимости обозначено отрезком АВ, касательным к поверхности Земли в т. С. Если рассчитывать поле в т. В по интерференционным формулам, то оно окажется близким к 0, т.к. прямой и отраженный луч в т. В окажутся в противофазе (Δr = 0, а q = p). Поэтому расчет поля по формуле (10.32) проводится до расстояний, несколько меньших r₀ (r £ 0,7 r₀), где r₀ – расстояние прямой видимости. На расстояниях r ³ 0,7 r₀ расчет поля проводится по дифракционным формулам (раздел 10.3.).

 Определим расстояния прямой видимости. Как видно из рис. 10.10,

,

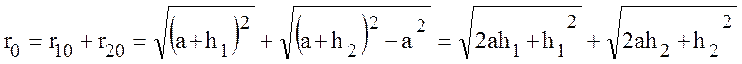где  а – радиус Земли, h₁ и h₂ – высоты установки антенн.

Так как   h₁ и h₂ << а, то окончательно:

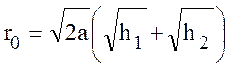                         .                                (10.40)

Учитывая, что средний радиус Земли а = 6370 км, формулу (10.12) можно записать в виде

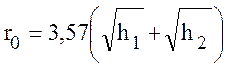          ,    км ,                              (10.41)

где   h_1, h₂  - в м.

Из формулы (10.41) следует, что расстояние прямой видимости при существующих на практике высотах расположения антенн (h составляет десятки и сотни метров) не превышает сотни км.

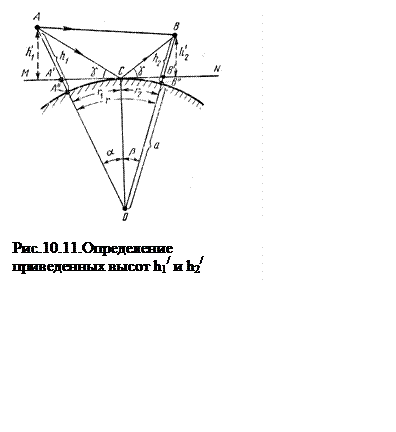
Учет сферичности Земли при расчете поля в случае высокоподнятых антенн производится посредством замены истинных высот установки антенн некоторыми условными величинами, называемыми приведенными высотами. Смысл сказанного раскрывается при рассмотрении рис. 10.11.

Не учитывая особенностей, возни-кающих при отражении луча от сфери-ческой поверхности в т. С, задачу рас-пространения волны вокруг сферической поверхности Земли можно заменить эквивалентной задачей о распростране-нии волны над плоской Землей при соответствующей коррекции высот уста-новки антенн. На рис. 10.11. приведенные высоты антенн h₁ и h₂ соответственно обозначены как h₁¢ и h₂¢. Поэтому в интерференционных формулах вместо истинных высот нужно подставлять значения приведенных высот. Очевидно, что при приближении длины радиолинии к расстоянию прямой видимости действующие высоты антенн стремятся к нулю, в результате чего напряженность поля также стремится к нулю, что еще раз подчеркивает эквивалентность подобной замены.

Приведенные высоты можно определить по известным значениям истинных высот h₁ и h₂, и расстоянию r. Учитывая реальные размеры Земли приведенные высоты можно определить приближенно так:

        h₁¢ ≈ h₁ – Δh₁,

                                 h₂¢≈h₂ – Δh₂.                                                    (10.42)

Так как r₁₀ соответствует расстоянию прямой видимости при высоте Δh₁, а r₂₀ соответствует расстоянию прямой видимости при высоте Δh₂, из формулы (10.40) находим:

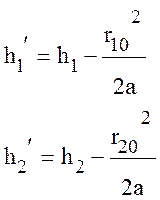                                                                  (10.43)