Распространение земных радиоволн, страница 3

В общем случае Земля ведет себя как полупроводящая среда, и даже тогда, когда кривизной земной поверхности можно пренебречь, задача о расчете поля поверхностной волны встречает большие математические трудности. Из первой части книги известно, что такая задача строго решается на основании волновых уравнений с учетом граничных условий. Первая попытка решить эту задачу была предпринята в 1909 г. А. Зоммерфельдом. Ограничиваясь случаем, когда в почве токи  проводимости преобладают над токами смещения, Зоммерфельд  получил выражение для напряженности поля в точке приема, которое оказалось столь громоздким, что пользоваться им для инженерных расчетов оказалось невозможно.

В 1923 г. М.В. Шулейкин придал решению Зоммерфельда вид, удобный для инженерных расчетов. В 1931 г. Ван дер Поль опубликовал формулу для расчета напряженности поля, практически совпадающую с формулой Шулейкина. С тех пор формула получила название формулы Шулейкина – ван дер Поля.

В дальнейшем был выполнен ряд работ, в которых формулы Шулейкина – ван дер Поля были обобщены на почве с любыми параметрами, получены графики и номограммы, облегчающие пользование расчетными формулами.

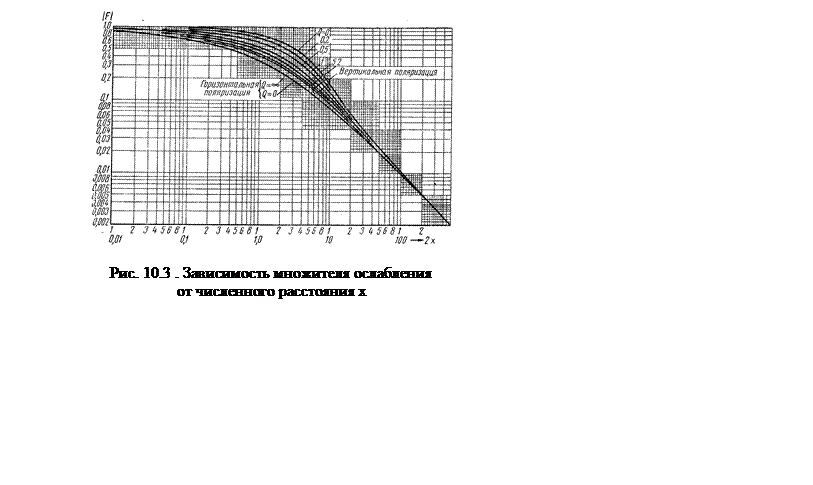
Множитель ослабления, полученный на основании строгого решения волновых уравнений, выражается функцией нескольких переменных (длины волны, длины трассы, параметров почвы), что весьма затрудняет проводить расчеты напряженности поля. Шулейкину и ван дер Полю громоздкое выражение для множителя ослабления удалось свести к более простому виду, где множитель ослабления является функцией одного переменного, названного численным расстоянием.

В общем случае формула Шулейкина – ван дер Поля имеет вид:

                               Е = Е₀F(х),                                        (10.4)

где  Е₀ – напряженность поля, определяемая по формуле для свободного пространства; х – численное расстояние, которое является безразмерной величиной и определяется из формулы:

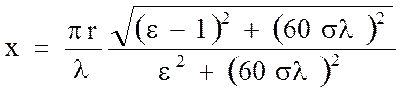                     ,                                     (10.5)

где  e – относительная диэлектрическая проницаемость Земли,

       s – удельная проводимость.

 В ряде случаев формуле (10.5) можно придать более простой вид. Для определенных видов поверхности Земли e >> 1. В то же время, на сверхдлинных, длинных и средних волнах практически для любого вида земной поверхности 60σl >> e. С учетом указанных допущений численное расстояние х можно определить по более простой формуле:

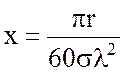                .                                                    (10.6)

В том случае, когда 60σl << e, численное расстояние можно определить из формулы:

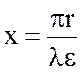                              .                                                   (10.7)

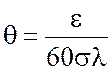На рис. 10.3 приведен график зависимости множителя ослабления от численного расстояния х для различных значений параметра , который значительно облегчает работу при практических расчетах.

Распространение волны над сферической поверхностью Земли.  На больших расстояниях от передатчика в расчетах напряженности поля поверхностной волны необходимо учитывать кривизну Земли, т.е. решать задачу о дифракции волны вокруг сферической поверхности. Строгое рассмотрение вопроса сводится к решению волновых уравнений в сферических координатах. Опуская сложные математические операции приведем окончательную дифракционную формулу для множителя ослабления:

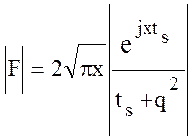                     .                                              (10.8)

Здесь q – параметр, который учитывает полупроводящие свойства поверхности Земли. Он определяется с помощью выражения:

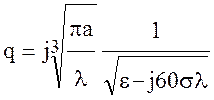                               .                                                 (10.9)

Для диапазона сверхдлинных, длинных и средних волн и высокопроводящей почвы, параметр q стремится к 0. В то же время в диапазоне УКВ и для почвы с j » 0, q стремится к бесконечности.

Параметр t_s представляет собой корни уравнения:

h^/(t) – qh(t) = 0,                                                   (10.10)