 Как
следует из полученной формулы, для определения множителя ослабления необходимо
знание трех неизвестных величин: модуля коэффициента отражения Г, угла сдвига
фазы волны при отражении q и
разности хода лучей Δr. Для определения первых двух
величин требуется знание вида поляризации, электрических характеристик земной
поверхности и угла скольжения отраженного луча. Модуль Г и фаза коэффициента
отражения q определяются с помощью
формул Френеля, подробное обсуждение которых приведено в первой части книги.
Угол скольжения луча, отсчитываемый от поверхности Земли и разность хода лучей
достаточно просто можно определить, воспользовавшись рис. 10.7.
Как
следует из полученной формулы, для определения множителя ослабления необходимо
знание трех неизвестных величин: модуля коэффициента отражения Г, угла сдвига
фазы волны при отражении q и
разности хода лучей Δr. Для определения первых двух
величин требуется знание вида поляризации, электрических характеристик земной
поверхности и угла скольжения отраженного луча. Модуль Г и фаза коэффициента
отражения q определяются с помощью
формул Френеля, подробное обсуждение которых приведено в первой части книги.
Угол скольжения луча, отсчитываемый от поверхности Земли и разность хода лучей
достаточно просто можно определить, воспользовавшись рис. 10.7.
Из треугольника А′В′В получим
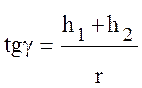 . (10.28)
. (10.28)
В большинстве практических случаев с достаточной точностью тангенс можно заме-нить его аргументом
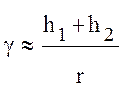 . (10.29)
. (10.29)
Разность хода лучей ∆r найдем из треугольников АВВ′ и В′ВА′ находим:
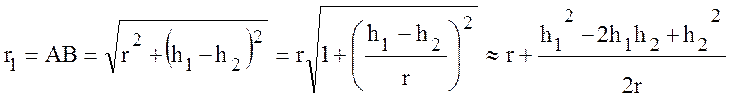 ,
,
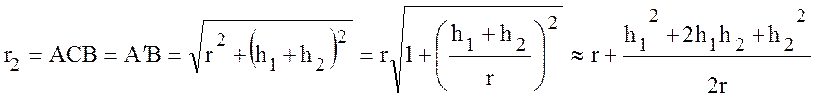
Разность хода лучей определяется как:
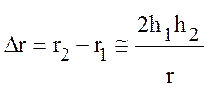 . (10.30)
. (10.30)
После подстановки (10.30) в (10.27) выражение для множителя ослабления примет окончательный вид
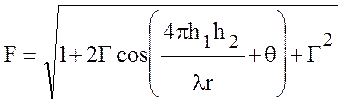 . (10.31)
. (10.31)
При изменении расстояния множитель ослабления
проходит последовательно через ряд максимумов и минимумов, что подтверждает
интерференционный характер поля. Максимумы функции F(r) находятся на расстояниях r, когда
аргумент косинуса 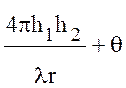 равен +1, а минимумы,
когда аргумент равен –1. Значения F в максимумах равны
(1 + Г), а минимумы – (1 – Г). Таким образом, величину F
называть множителем ослабления можно чисто условно, так как в максимумах она
больше единицы.
равен +1, а минимумы,
когда аргумент равен –1. Значения F в максимумах равны
(1 + Г), а минимумы – (1 – Г). Таким образом, величину F
называть множителем ослабления можно чисто условно, так как в максимумах она
больше единицы.
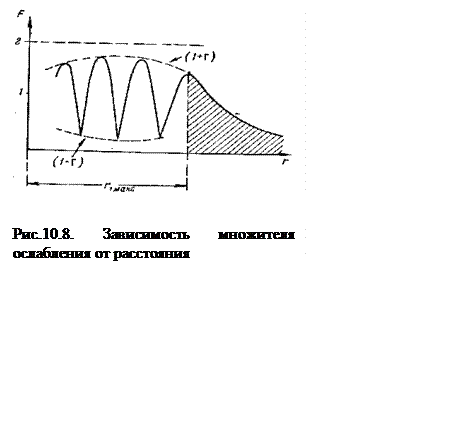 На
рис. 10.8. показан типичный ход зависимости множителя ослабления от
рассто-яния. Аргумент косинуса в формуле (10.23) является суммой двух
слагаемых. Первое слагаемое с ростом расстояния убывает, стремясь к нулю.
Второе – q, как следует из
законов Снеллиуса, стремится к p
независимо от электрических свойств почвы. Поэтому на некотором расстоянии от
источника излучения радиоволны аргумент косинуса становится равным 2p. При этом наступает последний максимум со
стороны больших расстояний. При дальнейшем росте расстояния угол q остается постоянным, и аргумент
косинуса в целом монотонно уменьшается, стремясь к p, а сам множитель ослабления F монотонно
уменьшается, стремясь к нулю.
На
рис. 10.8. показан типичный ход зависимости множителя ослабления от
рассто-яния. Аргумент косинуса в формуле (10.23) является суммой двух
слагаемых. Первое слагаемое с ростом расстояния убывает, стремясь к нулю.
Второе – q, как следует из
законов Снеллиуса, стремится к p
независимо от электрических свойств почвы. Поэтому на некотором расстоянии от
источника излучения радиоволны аргумент косинуса становится равным 2p. При этом наступает последний максимум со
стороны больших расстояний. При дальнейшем росте расстояния угол q остается постоянным, и аргумент
косинуса в целом монотонно уменьшается, стремясь к p, а сам множитель ослабления F монотонно
уменьшается, стремясь к нулю.
Во многих случаях формула (10.31) может быть подвергнута дальнейшему упрощению. При малых углах скольжения g для большинства видов земной поверхности модуль коэффициента отражения близок к единице, а его фаза - к 1800. Подставляя в формулу (10.31) Г = 1 и q = 1800 получим:
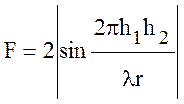 . (10.32)
. (10.32)
Расстояния, которым соответствуют максимумы множителя ослабления, можно найти из условия:
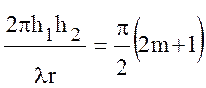 , (10.33)
, (10.33)
где m = 0, 1, 2, и т.д., откуда следует:
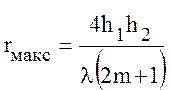 . (10.34)
. (10.34)
Последний максимум расположен при удалении от передатчика на расстоянии:
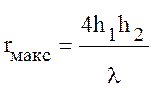 . (10.35)
. (10.35)
Месторасположение минимумов находится из условия:
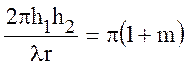 ,
, 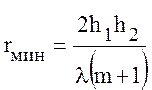 , (10.36)
, (10.36)
Последний минимум расположен на расстоянии от передатчика, равном
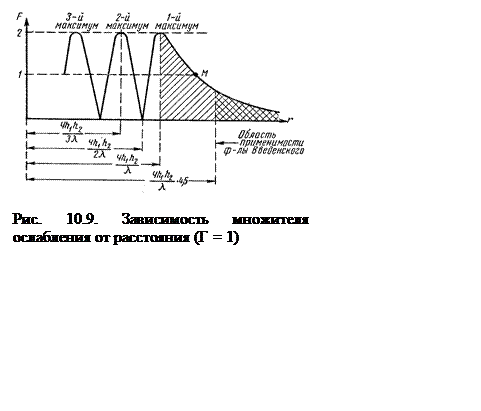
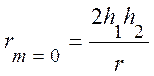 (10.37)
(10.37)
Изложенное выше иллюст-рируется рис. 10.9., из которого сле-дует, что в том случае, когда по-терь при отражении от Земли не происходит (Г = 1), значение мно-жителя ослабления в максимумах равно двум, а в минимумах – нулю.
Пример 10.2. Определить расстояние до последнего максимума множителя ослабления при следующих исходных данных: высота передающей антенны телецентра h1 = 180 м. Высота приемной антенны h2 = 20 м. Длина волны 2 телевизионного канала l = 4,8 м.
Для расчета воспользуемся формулой (10.35):
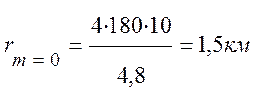 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.