Распространение земных радиоволн, страница 11

Судить о размерах первой зоны Френеля на отражающей плоскости можно в первом приближении при помощи построения, показанного на рис. 10.22. Действительный источник волн А заменяется по известному принципу его зеркальным отражением А¢. Следовательно, можно считать, что отраженный луч проходит путь А¢В.

На рис. 10.2. заштрихован эллипсоид, ограничивающий первую зону Френеля. В точке пересечения оси  А¢В с поверхностью Земли диаметр эллипсоида достигает значения 2b. Известно, что центральное сечение эллипсоида плоскостью имеет форму эллипса, причем при малых углах скольжения g размер MN много больше диаметра 2b.

Вводя прямоугольную систему координат, у которой ось X направлена вдоль большой оси эллипса (рис. 10.22.), и ограничиваясь случаем антенн равных высот над плоской поверхностью Земли, когда максимальные значения радиуса b зоны Френеля приходится на точку отражения, уравнение эллипса можно записать в виде:

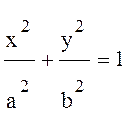                     .                                                                 (10.53)                  

Здесь через а обозначена большая полуось эллипса, равная приблизительно , где   r – протяженность трассы.

Уравнение прямой MN имеет вид:

,                                                    (10.54)

откуда абсцисса точки пересечения прямой MN и эллипса:

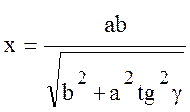                               ,  м.                                      (10.55)

В виду малости угла g размер x можно отождествлять с искомой большой полуосью эллипса СN на поверхности Земли. Малая полуось эллипса, ограничивающего первую зону Френеля на поверхности Земли, примерно равна величине b.

Размеры существенной области, в пределах которой формируется отраженная волна, довольно значительны, как это следует из рассматриваемого ниже примера.

Пример 10.3. Определить размеры области, ограниченной на поверхности Земли первой зоной Френеля, в пределах которой формируется отраженная волна, при следующих данных: длина трассы r = 50 км, высоты антенн h₁ =h₂= 50 м. По формуле (10.51) определим радиус первой зоны Френеля в случае, когда ₁ = ₂ = 25 км:

.

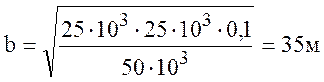По формуле (10.29) находим угол скольжения:

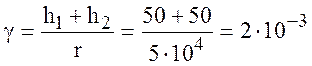(рад).

Подставляя вычисленные и заданные значения в формулу (10.25) и принимая, ввиду малости угла скольжения, a »  = 25×10³ м,получаем:

.

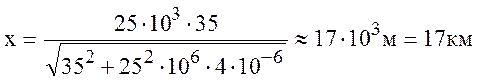В поперечном направлении малая ось эллипса, ограничивающего существенную область, равна 35 км.

Приведенный пример наглядно показывает, сколь значительны размеры области пространства на поверхности Земли, участвующего в создании отраженной волны. Вряд ли можно встретить холм с гладкой вершиной протяженностью в десятки километров.

Таким образом, при распространении радиоволн в условиях холмистой местности с зеркально отраженным лучом, как правило, можно не считаться. Задача проектировщика линии связи, проходящей в холмистой местности, заключается в таком выборе местоположения антенн и их высот, при котором существенная область целиком проходит над вершинами холмов. В подобных условиях холмы не будут порождать ослабления поля волны, множитель ослабления примет значение, равное единице, а само поле рассчитывается по формуле в свободном пространстве.

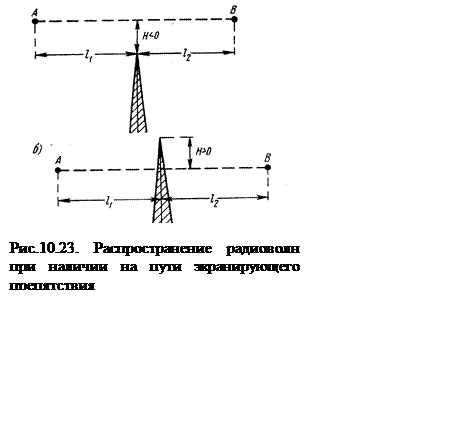Распространение радио-волн на линии с экрани-зирующими препятст-виями. В этом разделе речь пойдет о резко выраженных препятствиях, непрозрачных для радиоволн (остроконечные горные возвышенности, высотные здания т.д.). В таких условиях расчет поля нужно вести с помощью разработанного в физической оптике дифракционного метода.      На рис. 10.23. показаны два возможных случая распростране-ния радиоволн при наличии клинообразного препятствия. В первом случае препятствие не закрывает прямую видимость, а во втором – создает теневой эффект. Принято считать просвет отрицательным в первом случае (Н < 0) и положительным – во втором (Н>0).

Как следует из теории оптической дифракции, множитель ослабления имеет вид:

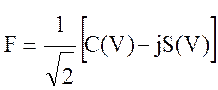,                              (10.56)

где  С(V) и S(V) – интегралы Френеля, определяемые по формулам: