Распространение земных радиоволн, страница 4

где  h(t) – известная из курса высшей математике функция Эйри, которая в табулированном виде представлена в математических справочниках специальных функций, а h¢ (t) – ее первая производная.

В заключении отметим, что ориентировочно область применения формулы Шулейкина – ван дер Поля можно определить из приближенной формулы:

,    км ,                                                      (10.11)

где l - в м.

 

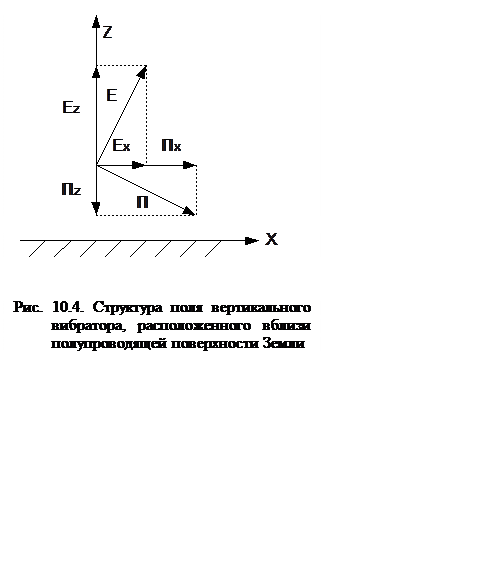
10.4. Структура поля земной радиоволны

в пункте приема

Исследуется структура поля земной волны в пункте приема.

 

При распространении радиоволны вдоль земной поверхности часть ее энергии проникает в глубь Земли, вызывая ее нагрев. Следовательно, кроме составляющей вектора Пойнтинга П_х, направленной вдоль поверхности Земли, имеется вертикальная составляющая П_у, направленная перпендикулярно к ее поверхности (рис.10.4.). В результате этого суммарный вектор Пойнтинга направлен под углом к поверхности Земли, а у вектора  имеется горизонтальная составляющая Е_х. Таким образом поверхностная волна не является поперечной в отличие от распространения в однородной среде.

Часто при расчетах напряженности поля земных волн применяют приближенные граничные условия (граничные условия Леонтовича), в основе которых лежит предположение, что модуль комплексной  диэлектрической проницаемости Земли много больше единицы 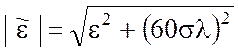>> 1.        (10.12)

Эти условия значительно упрощают решение волновых уравнений, а также существенно упрощают исследование структуры поля земной волны. Угол преломления волны на границе воздух - Земля нетрудно определить, применив закон Снеллиуса:

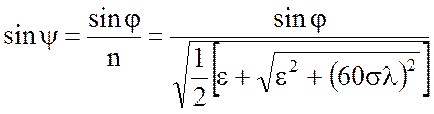,                                 (10.13)

где  n – коэффициент преломления земной поверхности.

Если >>1, то из формулы (10.13) следует, что угол преломления стремиться к нулю, т.е. волна в глубь Земли распространяется нормально к земной поверхности.

Как было показано в первой части книги, волна в среде имеет длину в n раз короче, чем длина волны в свободном пространстве:

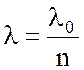 << l₀ .                                                   (10.14)

Согласно формуле (10.14) волна в толще Земли существенно укорачивается, в то время как на протяжении этой длины волны электромагнитное поле вдоль поверхности Земли практически не изменяется. Таким образом, преломленная волна является плоской однородной волной, которая распространяется в глубь Земли перпендикулярно ее поверхности.

На достаточно больших расстояниях от передатчика (kr >> 1) фронт волны можно приблизительно считать плоским. В итоге имеет место совокупность плоских волн, для которых можно применить все формулы, полученные в первой части учебного пособия.

Для плоской волны в Земле справедливо соотношение между напряженностями электрического и магнитного полей:

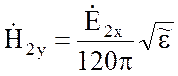.                                                       (10.15)

Согласно строгим граничным условиям, тангенциальные составляющие электрического и магнитного полей на границе раздела двух сред равны, т.е.:

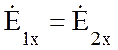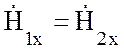           ,         .                                              (10.16)

C учетом формулы (10.15) можно записать:

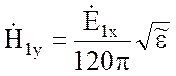                     .                                         (10.17)

Формула (10.17) является математическим выражением граничных условий Леонтовича.

В верхней среде (воздухе) для плоской волны справедливо соотношение:

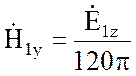                          .                                            (10.18)

Учитывая формулу (10.17), получим соотношение между вертикальной и горизонтальной составляющими напряженностями поля над границей раздела Земля – воздух.

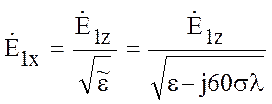          .                                    (10.19)

Строгие граничные условия (10.16) устанавливают связь между  и , откуда:

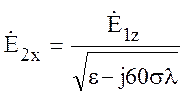                        .                                  (10.20)

Используя строгие граничные условия для нормальных составляющих электрического поля: