Распространение земных радиоволн, страница 5

,      где = 1,

определим  вертикальную составляющую этого поля в Земле:

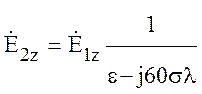               .                                          (10.21)

Из полученных формул (10.19, 10.20, 10.21) видно, что в воздухе вертикальная составляющая электрического поля больше горизонтальной, а у волны, распространяющейся в толще Земли, горизонтальная составляющая больше вертикальной.

Из формулы (10.19) следует, что горизонтальная и вертикальная составляю-щие электрического поля в воздухе имеют сдвиг по фазе. Таким образом, волна, распространяющаяся   над полупроводящей поверхностью Земли, имеет эллиптическую поляризацию (рис. 10.5.).

Этот факт объясняет возможность приема радиоволн вертикальной поляриза-ции на горизонтальный провод, ориентиро-ванный в направлении распространения волны. Именно это обстоятельство учиты-вается при использовании в качестве приемных  Г – образных антенн в диапазо-не длинных и средних волн.

 

10.5. Распространение радиоволн над поверхностью Земли

в случае высокоподнятых антенн

Исследуются вопросы расчета напряженности поля земной волны в случае высокоподнятых антенн.

 

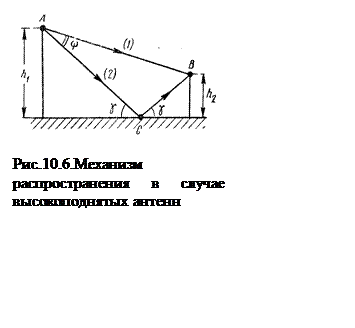
В диапазоне коротких и особенно ультракоротких волн антенны поднимают на высоты в десятки и сотни метров. Поэтому, как правило, выполняется условие h >> l. Следствием этого является то, что в пункт приема волна приходит по двум дискретно выраженным траекториям (рис. 10.6).

В дальнейшем эти траектории мы будем называть лучами, а сам механизм распространения – лучевым. Такая трактовка механизма распространения радиоволн позволяет для расчета поля использовать метод приближений геометрической оптики. Пусть волна распространяется над плоской, гладкой поверхностью Земли. Как видно из рис. 10.6., волна, излучаемая передающей антенной, расположенной в т. А, приходит к приемной антенне, расположенной в т. В по двум траекториям, т.е. двумя лучами – АВ и АСВ. Второй луч возникает в результате отражения волны от Земли. Все другие отраженные лучи в т. В не попадают в соответствии с законами оптики. Поле в т. В представляет собой сумму полей прямого и отраженного лучей . Учитывая, что всегда h₁ и h₂ << r, можно считать, что углы a и b достаточно малы и, поэтому результирующее поле равняется с достаточной точностью алгебраической сумме полей Е₁ и Е₂. Если радиоволна имеет нормальную (горизонтальную) поляризацию, то алгебраическое сложение полей ,  осуществляется автоматически. Таким образом,

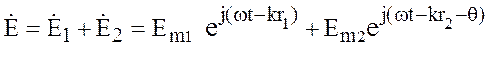,                          (10.22)

где  r₁ = АВ, r₂ =АСВ, а q – сдвиг фаз полей Е₁ и Е₂ возникший при отражении луча АВС от поверхности полупроводящей Земли. Как известно, коэффициент отражения в общем случае является комплексной величиной и выражается формулой:

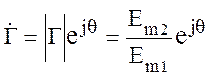                     ,                              (10.23)

где ½Г½ - модуль коэффициента отражения, который равен отношению амплитуды отраженной волны к амплитуде падающей волны. В то же время:

r₂ = АСВ = r₁ + Δr.

В последующих преобразованиях знак модуля коэффициента отражения для простоты будет опущен. С учетом (10.23) формулу (10.22) можно представить в виде:

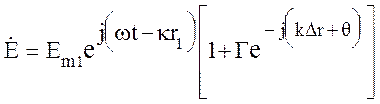,                (10.24)

где 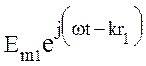  - известное выражение для напряженности поля радиоволны в свободном пространстве Е₀. Тогда с учетом формулы (10.4) величину 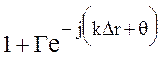 можно назвать коэффициентом ослабления F:

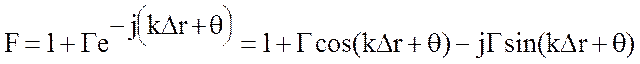 .                         (10.25)         

Модуль коэффициента ослабления равен:

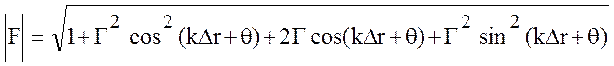 .            (10.26)

При расчетах амплитуды напряженности поля радиоволны фаза коэффициента ослабления принципиального значения не имеет и в дальнейшем исключается из рассмотрения. В последующем использовании формулы (10.26) знак модуля будет опущен для упрощения записи. В окончательном виде выражение для множителя ослабления принимает вид:

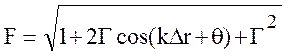   .                                         (10.27)