Распространение земных радиоволн, страница 8

Нетрудно заметить, что как в полную интерференционную формулу, так и в ее упрощенные варианты входит произведение действительных высот антенн h₁h₂. Поэтому при практических расчетах для учета сферичности Земли, нет необходимости определять значения приведенных высот каждой из антенн в отдельности. Достаточно уметь определять произведение приведенных высот h₁`h<sub>2</sub>`. Сделать это можно при помощи графика рис. 10.12., который позволяет определить поправочный коэффициент m в формуле:

                               h₁¢ h₂¢ = mh₁h₂  ,    м².

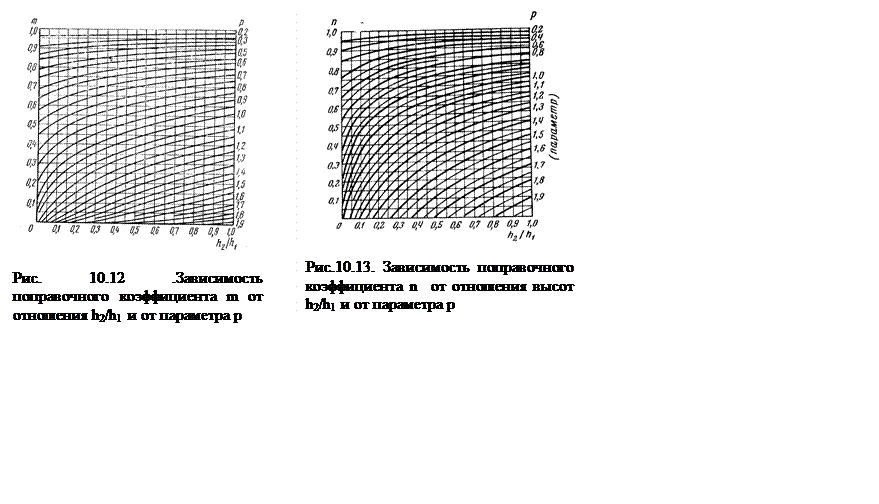Через h₁ обозначена бόльшая высота, независимо от того, является ли эта антенна передающей или приемной. Параметром  р служит величина:

,

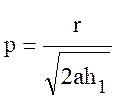где   r, а, h – в м.

Значения поправочного множителя m отсчитываются по оси ординат.

Аналогичным образом по графику на рис. 10.13., вычисляют поправочный множитель n к формуле для определения угла скольжения:

.

 

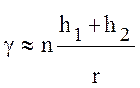10.6. Распространение радиоволн над неровной

поверхностью Земли

Вводится понятие критерия Релея, зон Френеля и области пространства, существенно участвующей в распространении радиоволн.

 

Критерий  Релея. Лишь для очень длинных волн поверхность Земли условно может считаться гладкой. На сантиметровых и миллиметровых волнах даже травяной покров или небольшая рябь на поверхности моря представляет собой неровную поверхность, не говоря уже о горных хребтах, пересеченной местности или лесных массивах. Крупные и мелкие населенные пункты, отдельные застройки и различные сооружения могут также входить в определение неровной поверхности Земли. Это обстоятельство требует уточнения существующих методов расчета напряженности поля земных волн или же создания новых методов.

Применение того или иного метода расчета на практике предваряется оценкой степени неровности Земной поверхности на конкретной трассе радиосвязи. Эта оценка производится с помощью метода, называемого критерием Релея.

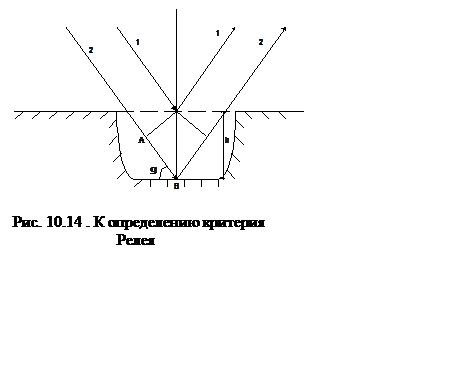
На рис. 10.14. изображена поверхность с неровностью в виде впадины. В отличие от луча 1, отраженного от воображаемой гладкой поверхности (пунктир), луч 2, отраженный от дна впадины, запаздывает относительно луча 1 по фазе на величину:

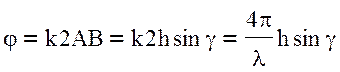                     ,                            (10.44)

где 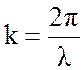,  h – глубина впадины.

Таким образом, критерием неровности поверхности может служить величина j.

Если положить 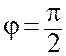, то из (10.44) можно определить величину неровности h, соответствующую фазовому сдвигу j:

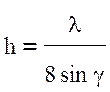.                (10.45)                                                                                    

Принято считать, что если j < , то поверхность является гладкой, если j >  - неровной. Формула (10.45) является математическим выражением критерия Релея.

Как видно из формулы (10.45), кроме относительной высоты неровностей  на степень неровности поверхности влияет также и угол скольжения лучей g. Для более пологих лучей поверхность представляется более гладкой.

Отражение волны от неровной поверхности теряет чисто зеркальный характер (рис. 10.15.). Появляются диффузно рассеянные лучи, общий уровень которых растет по мере увеличения относительной высоты неровностей и увеличения угла скольжения. Это явление сопровождается соответствующим уменьшением уровня зеркального отраженного луча. Поэтому при расчете поля поверхностной волны следует внести поправки в значение коэффициента отражения.

     В настоящее время еще не разработано на-дежных методов расчета коэффициента отражения от неровной поверхнос-ти, поэтому на практике пользуются значениями, определенными экспери-ментально  для различного типа неровностей (лесные массивы, горные местности, морская поверхность при различной силы волнениях и т. д.).

В качестве примера в табл. 10.2. приведены значения коэффициента отражения для одного из видов земной поверхности.

Таблица 10.2.