Влажность воздуха. Характеристика жидкого состояния вещества. Характеристика твердого состояния вещества. Плавление и кристаллизация, страница 22

Линейное расширение твердых тел при нагревании. Вспомним, что кристаллы обладают анизотропией, поэтому, вообще говоря, величина расширения кристалла при нагревании зависит от направления.

Однако большинство твердых веществ имеют поликристаллическое строение, и потому они являются изотропными. Все изложенное  дальше в этой главе относится к изотропным телам.

Итак, расширение твердых веществ при нагревании происходит одинаково по всем направлениям. Однако во многих случаях на практике приходится учитывать расширение только в одном направлении. Например, при прокладке труб для провода приходите учитывать удлинение этих труб при нагревании, а изменение площади поперечного сечения стенок труб, практического значения не имеет. Изменение одного определенного размера твердого тела при изменениях температуры называется линейным расширением (линейным сжатием).

Пусть имеется стержень, длина которого при 0°С равна l₀, а при температуре t равна l_1. Следовательно, изменение длины стержня при его нагревании на ∆t=t-0=t будет равно ∆l=l_t-l₀ - На основании опытов легко установить, что изменение длинны стержня ∆1 прямо пропорционально приросту температуры Δt и его длине 1₀ при О °С, т.е.

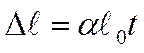                                      (1)

Зависимость ∆l от рода вещества выражается коэффициентом пропорциональности .

Величина α, характеризующая зависимость линейного расширения при нагревании от рода вещества и внешних условий, называется коэффициентом линейного расширения. Коэффициент линейного расширения показывает, на какую часть длины тела, взятого при О °С. изменяется его длина при нагревании на 1 °С:

                                            а = (∆l)/l_ot                 (1a)                                                

Найдем формулу, позволяющую вычислить длину тела при различных температурах по известной длине lo . Из (1) имеем

                                                (2)                                                 

Чтобы по длине тела l₁ при температуре t₁ найдем его длину l₂ при температуре t_2, вообще говоря, сначала нужно найти l₀ с помощью формулы (2), а затем по этой же формуле вычислить l₂. Однако, учитывая, что  - очень маленькое число, l₂ можно находить по следующей приближенной формуле:

(3)

из формулы (3) получаем приближенную формулу для вычисления коэффициента линейного расширения твердого вещества:

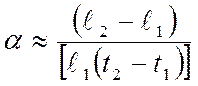
(3a)                    

Объемное расширение тел при нагревании

 Зависимость плотности вещества от температуры

Пусть при О °С и при температуре t объемы какого-либо тела соответственно равны V₀ и V_t -Тогда изменение объема тела в процессе повышение температуры на ∆t=t-0=t будет ∆V =V_t-V₀. Опыт показывает, что это изменение объема тела прямо пропорционально приросту температуры и начальному объему Vo:

                                                  ∆V=β V_ot(4)

Величина β, характеризующая зависимость объемного расширения тела при нагревании  от рода вещества и внешних условий, называется коэффициентом объемного расширения, Коэффициент объемного расширения показывает, на какую часть объема тела, взятого  при °С, изменяется объем этого тела при нагревании на1 °С:

             β=(∆V)/V₀t.                         (4а)

Формула (4) позволяет легко получить зависимость объема тела от температуры:

                    V_t-V_o = βV₀t, или V_t=V₀(1+ βt).         (5)

Если известен объем тела V₁при температуре t₁ ,то его объем V₂ при температуре t₂можно находить по приближенной формуле:

                       V₂ ≈V_t[1+ β (t₂-t₁)]                 (6)

Из (6) получаем приближенную формулу для вычисления коэффициента объемного расширения:

                               β ≈(V₂-V₁)/V₁ (t₂-t₁)    (6а)

отметим, что все формулы справедливы, если масса тела при 0°С изменение температуре остается постоянной. Это означает, что плотность вещества должна зависеть от температуры, поскольку объем меняется с температурой.

Действительно, плотность вещества при 0°С выражается формулой ρ₀=m/ V₀ ,a при температуре t -формулой