Перекачка высоковязкой и застывающей нефти, страница 25

2.3.7.3. Общий случай определения оптимальных параметров

“горячей” перекачки по теплоизолированному трубопроводу

При оптимизации температурного режима перекачки, толщины тепловой изоляции, числа пунктов подогрева и насосных станций необходимо учитывать следующие ограничения:

1) число пунктов подогрева N_тс и насосных станций n должно быть целым;

2) толщина тепловой изоляции не должна быть меньше минимально допустимой (по технологическим соображениям) величины,  т.е. ;

3) начальная и конечная температуры нефти не должны выходить за пределы допустимых значений, то есть Т_н £ [Т_н] и Т_к  ³ [Т_к];

Ранее рассмотренные подходы к оптимизации отдельных параметров “горячей” перекачки этих ограничений не учитывают. Поэтому нами был предложен следующий алгоритм одновременной оптимизации всех параметров “горячих” теплоизолированных трубопроводов.

Из имеющегося опыта проектирования “горячих” трубопроводов известно, что нефтеперекачивающие станции на них удалены друг от друга на расстояние от 50 до 150 км. Это позволяет назначить пределы варьирования числа НПС от 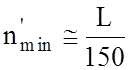 до 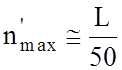. Найденные значения округляем до ближайших целых  и . Соответственно расстояние между НПС будет находиться в пределах

от 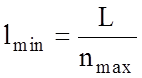 до .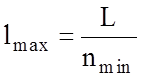

Полагая число пунктов подогрева кратным числу нефтеперекачивающих станций, можем найти

                                     ,

где   - средний коэффициент кратности числа пунктов подогрева числу НПС,  ³ 1 и принимает только целые значения.

Таким образом, первое ограничение непосредственно вносится в алгоритм расчета.

При заданной производительности трубопровода выбор насосов и определение их количества на НПС не представляет труда. Следовательно, напор насосной станции Н_ст известен. Согласно уравнению баланса напоров, он полностью расходуется на преодоление трения и разности нивелирных высот на перегоне между станциями. Так как точная величина Dz_ст  нам неизвестна примем в расчете ее определенное значение 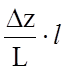. Тогда уравнение баланса напоров для участка трубопровода между пунктами подогрева примет вид

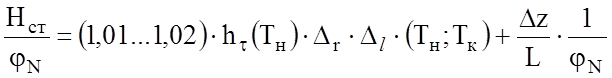.               (2.49)

В нем 2 неизвестные: Т_н и Т_к  . В качестве дополнительного условия используем уравнение Шухова

.

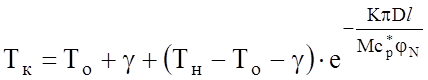Перед нами 2 уравнения с 3 - мя неизвестными: Тн, Т_к  и К. Последняя величина зависит от толщины тепловой изоляции. Задаваясь ей с учетом второго ограничения, а также величинами l и , можем решить эти два уравнения методом последовательных приближений относительно Т_н и Т_k . Таких пар связанных друг с другом начальной и конечной температур мы получим столько сколько зададим вариантов величины Т_н. Те пары, в которых Т_н и Т_к  не  удовлетворяют наложенным ограничениям, отбрасываем. То есть сразу учитываем третье ограничение.

Таким образом расчет будет выполнен по числу  вариантов

                            ,

где    -число рассматриваемых вариантов по числу

         насосных станций, коэффициенту кратности, толщине тепловой

         изоляции и начальной температуре (подогрева) в отдельности.

Для каждого варианта вычисляются суммарные приведенные затраты на насосные станции, пункты подогрева и тепловую изоляцию трубопровода. Оптимальные параметры для заданного диаметра трубопровода соответствуют минимальным приведенным затратам.Число вариантов расчета можно уменьшить, введя упрощающее допущение. В чем оно состоит? Многочисленные расчеты показывают, что с достаточной точностью гидравлический расчет “горячей” перекачки можно выполнять по формулам, справедливым для изотермического течения, но при этом вязкость, плотность и расход нефти надо брать при средней температуре перекачки (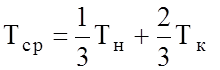; справедливо при Ш_у = 3). Поэтому примем, что

                        .

Учитывая, что при последующей расстановке насосных станций и пунктов подогрева температуры Т_н и Т _к будут корректироваться, погрешность такого допущения практически сводится к нулю.

Оно дает нам существенное упрощение оптимизационного расчета. В этом случае уравнение баланса напоров имеет вид

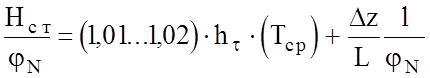.             (2.50)