Перекачка высоковязкой и застывающей нефти, страница 22

Рассмотрим частный случай оптимизации величин Т_н и Т_k для уже построенного “горячего” трубопровода, диаметр которого известен, а насосные и тепловые станции расставлены по трассе. Наиболее общее решение задачи об оптимизации температурного режима перекачки в этом случае получено В.С. Яблонским в 1956 г.

Так как все капитальные вложения уже сделаны, оптимизация Т_н и Т_к выполняется из условия минимизации эксплуатационных расходов, связанных с температурным режимом перекачки, а именно платы за энергию, потребляемую на перекачку и подогрев нефти.

Стоимость энергии, затрачиваемой в единицу времени на перекачку, равна

                                     ,

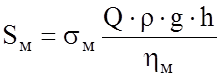где     - стоимость единицы механической энергии;

         h - полные потери напора на участке между пунктами подогрева;

         - к.п.д. насосных агрегатов.

Стоимость тепловой энергии, затрачиваемой в единицу времени на подогрев нефти, составляет

 

                                     ,

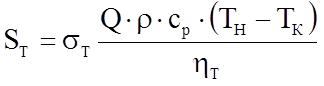где    s_т - стоимость единицы тепловой энергии;

         h_т - к.п.д. нагревательных устройств.

Профессор Яблонский В.С. выразил полные потери напора h как сумму потерь напора на турбулентном и ламинарном участках течения нефти между пунктами подогрева, определил производную 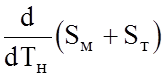, приравнял её нулю и получил в итоге условие для определения оптимальных Т_н и Т_к   вида

на последней единице длины трубопровода

на первой единице длины трубопровода

 

                                                                                                         (2.33)

где     соответственно гидравлический уклон и полный коэффициент теплопередачи на начальном участке трубопровода;

         i_к, К_к - то же для конечного участка.

Полученное условие В.С. Яблонский сформулировал так: “При оптимальном значении начальной и конечной температуры сумма стоимостей энергий, затрачиваемых на перекачку и подогрев на первой единице длины нефтепровода, равна такой же сумме, вычисленной для последней единицы длины нефтепровода”.

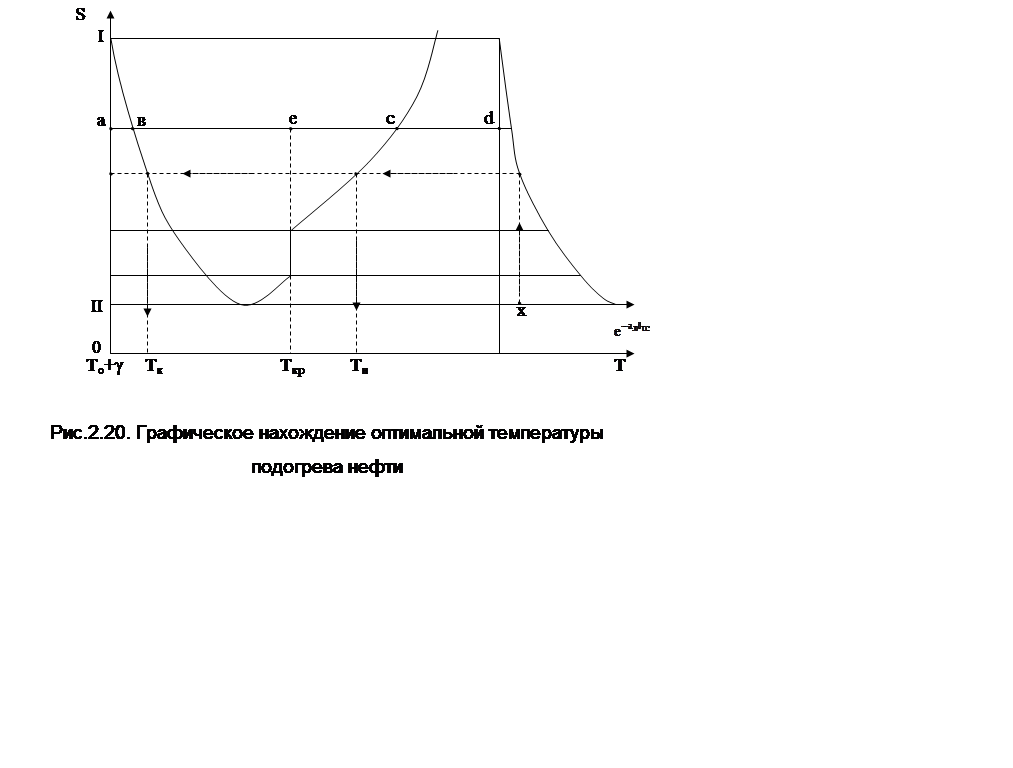
На основании полученного аналитического решения оптимальная температура подогрева сравнительно просто определяется следующим графо-аналитическим методом (рис. 2.20). Строится график зависимости от температуры Т функции

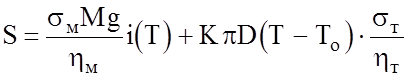.                     (2.34)

Нетрудно видеть, что значения Т_н и Т _к, удовлетворяющие уравнению (2.33), лежит на горизонталях, проведенных при S = const. Видно также, что таких пар можно подобрать сколько угодно. Какое же их сочетание является искомым?

Из бесчисленного множества парных значений Т_н и Т_к, отвечающих на графике условию S(Т_н) = S(T_k), надо выбрать пару, связанную между собой законом температуры по длине трубопровода.

 

В качестве аргумента для вспомогательного графика целесообразно выбрать величину . При ламинарном режиме все просто

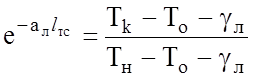                                     .                    (2.35)

При турбулентном режиме немного сложнее

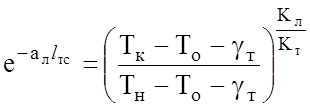                                      .             (2.36)

При смешанном режиме течения вывод продемонстрируем полностью.

Для турбулентного участка

                                     ,

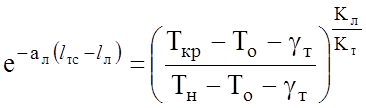а для ламинарного

.

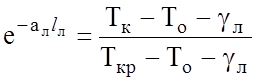Перемножив соответственно левые и правые части данных выражений получаем

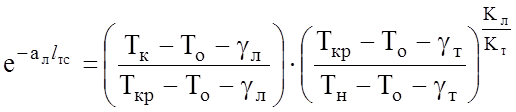.        (2.37)

Но откуда нам взять искомые величины Т_н и Т_k?  Ответ на  этот вопрос таков. Если с учетом погрешности построений пренебречь разницей между величинами g_л и g_т, то соотношение разностей температур можно заменить соотношениями длин отрезков, взятых с основного графика. Так, для горизонтали ad отношение (Т_н -Т_о - g)/ (Т_k -Т_о - g) с точностью до погрешности построений равно соотношению длин отрезков ас и аb.

Пользуясь этим методом для каждой из проведенных горизонталей, по формулам (2.35) и (2.37) вычисляем  и в масштабе откладываем на продолжении этих линий. Соединив полученные точки, будем иметь кривую, являющуюся ключом к решению поставленной задачи.