Перекачка высоковязкой и застывающей нефти

 

Для ньютоновских жидкостей кривая течения имеет вид прямой, выходящей под углом из начала координат, и описывается уравнением Ньютона

                                           ,                                    (2.1)

где коэффициент пропорциональности m, характеризующий угол наклона кривой течения, есть ни что иное как динамическая вязкость жидкости.

Модуль скорости сдвига в данном уравнении появляется из-за того, что отсчет текущего радиуса r ведется от оси трубы и поэтому величина 

 <  0, тогда как t - величина только положительная.

Пользуясь этими зависимостями легко получить характер распределения касательных напряжений по сечению трубопровода: t = 0 на оси и         t = t_max на стенке трубы. Для характеристики реологических свойств ньютоновских жидкостей достаточно знать их вязкость, плотность и температуру застывания (замерзания).

Значительно большое количество жидкостей отнесено к классу неньютоновских. В него объединены все те жидкости, кривая течения которых отличается от кривой 1.

Неньютоновские жидкости, в свою очередь, делятся на

- пластичные (или бингамовские);

- псевдопластичные;

- дилатантные.

       Кривые их течения обозначены индексами соответственно 2, 3, 4.

Как видно из рисунка, течение бингамовских жидкостей начинается только после создания определенного напряжения t_о, называемого начальным напряжением сдвига. При меньших, чем t_о, напряжениях такие жидкости ведут себя, как твердые тела, а при больших - как ньютоновская жидкость, для которой напряжение сдвига равно t - t_о. Из характера кривой течения нетрудно видеть, что для бингамовского пластика зависимость напряжения от скорости сдвига, описывается уравнением

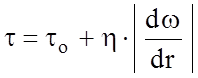                                     .                            (2.2)

Это уравнение Шведова-Бингама. Здесь h - так называемая пластическая вязкость (аналог динамической вязкости при ).

Для псевдопластичных и дилатантных жидкостей в широком диапазоне изменения скорости сдвига можно применять степенную зависимость напряжения от скорости сдвига

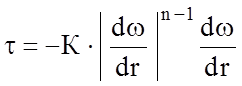                 или 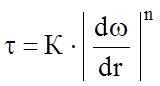     ,           (2.3)

где К и n - постоянные для данной жидкости коэффициенты. Коэффициент К называется характеристикой консистентности, а n - индексом течения.

Из характера кривых течения нетрудно видеть, что для псевдопластиков n < 1, а для дилатантных жидкостей n > 1. Кроме того, видно, что уравнение кривой течения ньютоновских жидкостей представляет собой частный случай уравнения (2.3) когда К = m, а n = 1. Отсюда становится ясным физический смысл коэффициентов: К - коэффициент, характеризующий вязкость жидкости; n - показатель степени, характеризующий меру отклонения поведения жидкости от ньютоновского.

Обобщает все вышеназванные зависимости реологическая модель Балкли-Гершеля

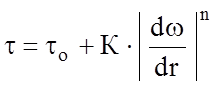                                     .                         (2.4)

Кривые течения 2 и 3 характерны для парафинистых нефтей и нефтепродуктов при температурах, близких к температуре их застывания или замерзания. При высоких температурах они ведут себя как ньютоновские жидкости. Так исследования реологического поведения топочного мазута М-100 и ряда вязких масел показало, что они сохраняют ньютоновское поведение при следующих температурах: мазут - выше +35 ^оС, трансмиссионные масла летнее и зимнее, авиационное масло МС-20 - выше +10 ^оС, цилиндровое 52, компрессорное масло КС-19 и автомобильное АС-10 - выше  0 ^оС.