Рудничный транспорт для разработки шахты "Красноярская", страница 5

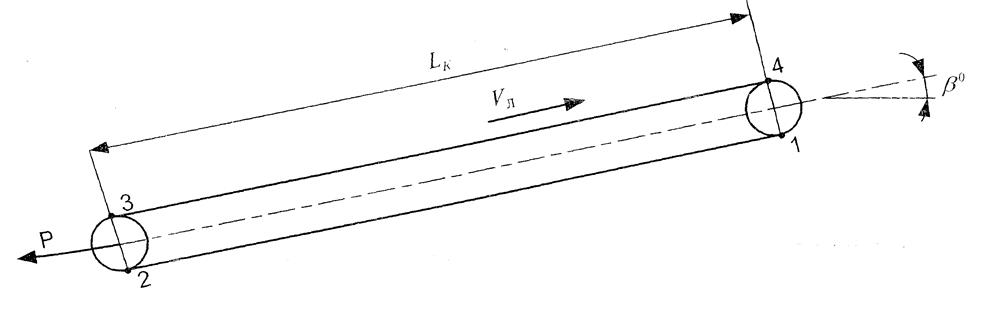
Рис. 3.6. Расчетная схема ленточного конвейера 2Л-100

Тяговой расчет произведем в соответствии с рекомендациями [3, стр. 10] в следующей последовательности:

Значение массы груза, приведенной к одному погонному метру конвейера q_г (кг/м) определяется по формуле:

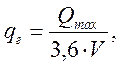(3.17)

                                            

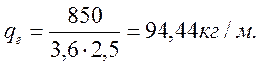
Значения сил сопротивления движению верхней и нижней ветвей ленты определяется по формуле:

  Для незагруженной верхней ветви:

W_вп = L_к ∙ g ∙ [(q_л + q'_p) ∙ ω_э ∙ cosβ + q_л ∙ sin β],                     (3.18)

где ω_э – эквивалентный коэффициент сопротивления движению ленты;                                                                 ω_э = 0,035.

Подставив в формулу (3.18) соответствующие значения получим:

W_вп = 1170 ∙ 9,81[(37 + 20,4) ∙ 0,035 ∙ cos 4˚ + 37 ∙ sin 4˚] =               = 17053,62 Н.

 

  Для загруженной верхней ветви:

W_вз = L_к ∙ g ∙ [(q_г + q_л + q' _p) ∙ ω_э ∙ cosβ + sin β (q_г + q_л)],       (3.19)

Подставив в формулу (3.19) соответствующие значения получим:

W_вз= 1170 ∙ 9,81[(94,44 + 37+ 20,4) ∙ 0,035 ∙ cos 4˚+ sin4˚(37+      + 94,44)] = 57432,49 Н.

  Для нижней ветви:

W_н = L_к ∙ g ∙ [(q_л + q"_p) ∙ ω_э ∙ cosβ + q_л ∙ sin β],                        (3.20)

Подставив в формулу (3.11) соответствующие значения получим:

W_н= 1170 ∙ 9,81[(37 + 3,6) ∙ 0,035 ∙ cos(–4˚) ± 37 ∙ sin(–4˚)] =               = –32933,9 Н.

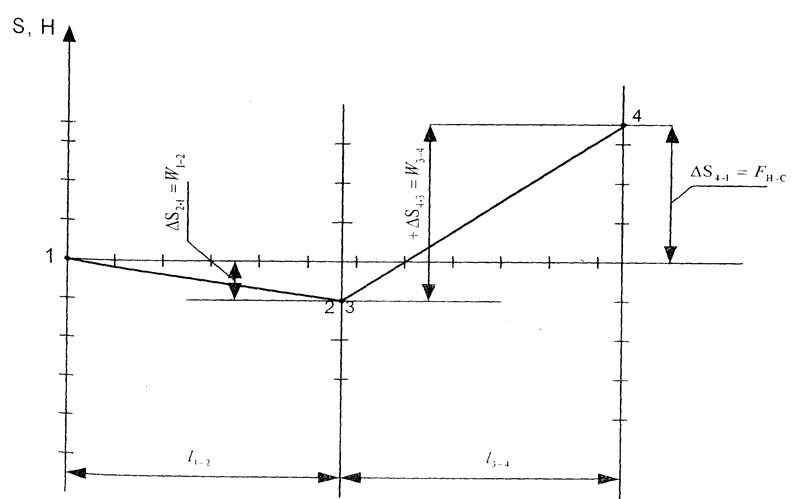
Рис. 3.7. Недостроенная диаграмма натяжения ленты бремсбергового     конвейера 2Л-100

При расчете по формулам (3.18), (3.19) и (3.20) знак угла β принимается " + " при движении вверх и " – " при движении вниз.

Тягловое усилие привода F_н.с определяется как алгебраическая сумма приращений натяжений ленты на участках замкнутого контура между точками с натяжением S_нб(S₄)  и S_сб(S₁).

F_н.с = Σ_Δ S_4-1 = _Δ S_1-2 + _Δ S_3-4,                                   (3.21)

где Σ_Δ S_4-1 – сумма приращений в контуре ленты между точками сбегания и набегания ленты на приводном барабане.

Подставив в формулу (3.21) соответствующие значения получим:

F_н.с = –32933,9 + 57432,49 = 24498,59

Так как F_н.с положительно, то приводной двигатель работает в двигательном режиме.

Условие отсутствия пробуксовки  на приводном барабане.

Это условие выполняется, если минимальная величина натяжения ленты S_{сб min} в точке сбегания с приводного барабана при положительной величине F_н.с удовлетворяет условию:

S_{сб min} = S_{1 min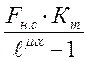} ≥                                        (3.22)

где К_т – коэффициент запаса тяговой способности привода;                                        исходя из рекомендаций [3, стр. 15], примем К_т = 1,35.

Тогда формула примет вид:

S_{сб min} = S_{1 min} ≥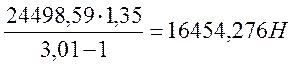

Условия отсутствия чрезмерного провеса ленты между роликоопорами.

 

Излишний провес приводит к потере каркасности ленты, повышенным изгибным напряжениям, увеличению сопротивления движению. Исходя из допустимой величины провеса ленты минимальная величина ее натяжения    S_{г min} в точке наименьшего натяжения на грузовой ветви, в соответствии с рекомендациями [3, стр. 16], должна быть не менее, чем определенная по формуле:

 ≥ 8 ∙ g (q_г + q_л) ∙ l'_p,                                  (3.23)

для порожней ветви:

 ≥ 8 ∙ g ∙ q_л ∙ l"_p,                                     (3.24)

Подставив в формулы (3.23) и (3.24) соответствующие значения получим:

 ≥ 8 ∙ 9,81 (94,44 + 37) ∙ 1,5 = 15473,11 Н

 ≥ 8 ∙ 9,81 ∙ 37 ∙ 3,0 = 8711,28 Н.

Эти два условия учитываем при нанесении оси абсцисс на диаграмме натяжения ленты.

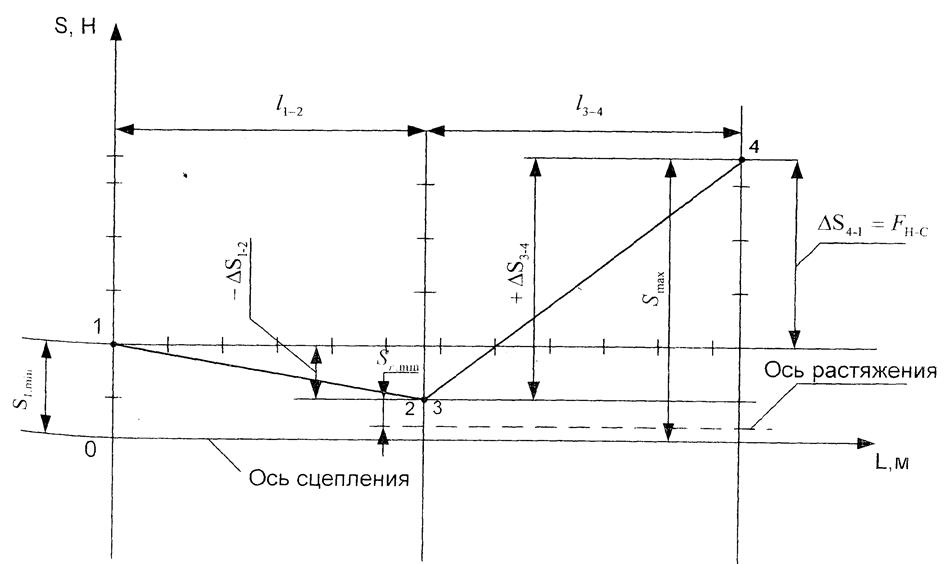
Рис. 3.8. Полная (достроенная) диаграмма натяжения ленты

бремсбергового конвейера 2Л-100

Определение максимальной величины натяжения ленты.

По диаграмме натяжений определим величину максимального натяжения ленты S_max, проводя отсчет от оси абсцисс (оси сцепления).

Алгебраически S_max определяется как сумма приращений натяжений ленты на участках замкнутого контура:

S_max = S_{сб min} + _Δ S_1-2 + _Δ S_3-4,                               (3.25)

Подставив в формулу (3.25) соответствующие значения получим: