Арифметичні основи цифрової техніки (Глава 1 навчального посібника), страница 6

§1.3. ЦИФРОВІ КОДИ

1.3.1. Загальні відомості

Різноманітну інформацію: цифрові дані, адреси, друкарські символи, команди тощо обчислювальні пристрої сприймають як повідомлення або слова у вигляді двійкових чисел – цифрових кодів. Цифровий код – це сполучення за певними правилами символів 0 та 1 для відображення повідомлення. Сенс кодів тлумачиться в ЕОМ залежно від виконуваної операції, наприклад, як операнди  (числа) під час арифметичних дій, як логічні змінні для виконання логічних операцій, як коди літер після команди “Друкувати” тощо.

Мета кодування полягає в тому, аби забезпечити простоту, надійність зберігання та обробки інформації, мінімум обладнання, узгодження із зовнішніми пристроями, високі швидкодію та вірогідність передавання  й оброблення повідомлень, полегшити сполучення людини з ЕОМ і т. ін. За умов протиріччя окремих вимог задовольняють головні з них для конкретної системи, тому й існує багато кодових різновидів.

За формою передавання й приймання по каналах сполучення  розрізняють послідовні коди (коли розряди надходять послідовно в часі однодротовою лінією) та паралельні (коли всі розряди слова передаються одночасно багато-дротовою лінією – шиною).  Послідовні цифрові коди потребують менше обладнання і більш завадостійкі, тому застосовуються, головним чином, для сполучення з віддаленими об'єктами. У радіотехнічних та обчислювальних пристроях використовуються переважно паралельні коди, бо вони забезпечують значно вищу швидкодію. Природно, існує й комбінована форма кодів, коли довге слово приймається та обробляється за кілька заходів, наприклад, байтами.

З метою уніфікації та спрощення обладнання для виконання арифметичних операцій над числами зі знаком застосовують прямий, обернений або доповняльний арифметичні коди. На відміну від арифметичних, комбінаторні коди використовують для позначення літер, знаків, іншої нечислової інфор мації. Кодуванням цифр однієї СЧ за допомогою цифр іншої утворюються складені коди, наприклад, двійково-десяткові. Спеціального застосування в   лічильних пристроях, аналого-цифрових перетворювачах набули відбиті (рефлексні)  коди. Підвищити завадостійкість під час передавання інформації можна за допомогою завадостійких кодів, що дозволяють виявляти й виправляти помилки.

1.3.2. Арифметичні коди зображення чисел зі знаком

Прямий код є звичайне двійкове число з додаванням знакового  біта         (рис. 1.6): 0 – для додатних чисел та 1 – для від'ємних:

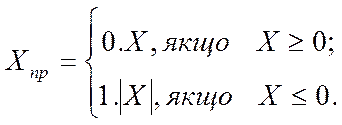
Приклади. 1) X=+10112; Xпр=0.1011; 2) X=-10112; Xпр=1.1011.

В ЕОМ подання чисел зі знаковим бітом трактується як мішаний дріб, в якого цей біт є цілою частиною. Це ніяк не впливає на виконання арифметичних дій, тому далі для зручності вважатимемо всі числа цілими.

Обернений або інверсний код додатного числа збігається з його прямим кодом, а від'ємного (див. рис. 1.6) – утворюється додаванням одиниці в знаковому розряді та оберненням або інвертуванням Х (взаємно оберненим заступленням одиниць нулями, а  нулів – одиницями) цифрової частини:

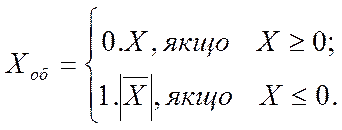
Приклади. 1) X=+10112; Xоб=0.1011; 2) X=-10112; Xоб=1.0100.

Природно, для перетворення оберненого коду від'ємного числа в прямий досить знов зінвертувати цифрову частину, тобто взаємно замінити в ній нулі та одиниці.

Доповняльний код уживається для виконання арифметичних дій найширше. У десятковій системі числення доповнення n-розрядного числа X10 є 10n-|X10|, наприклад, доповненням -18310 буде 81710. Так само й у двійковій системі з огляду на те, що

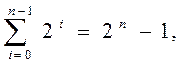
маємо доповнення n-розрядного числа

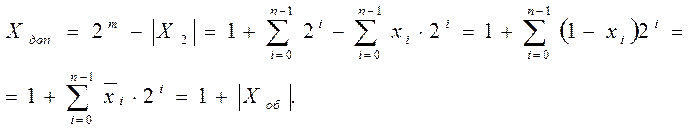
Таким чином, доповняльний код від'ємного числа (див. рис. 1.6) утворюється  за допомогою одиниці в знаковому розряді, інвертування цифрової частини та додавання одиниці до молодшого розряду, а код додатного числа збігається з прямим кодом: