Арифметичні основи цифрової техніки (Глава 1 навчального посібника), страница 2

вісімковою системами числення

Недолік двійкової СЧ – незручність запису довгих чисел – компенсується широким запровадженням шістнадцяткової та вісімкової систем для сполу­чення між пристроями цифрової техніки. Саме ці СЧ вибрано тому, що між ними й двійковою системою найлегше виконати перетворення чисел.

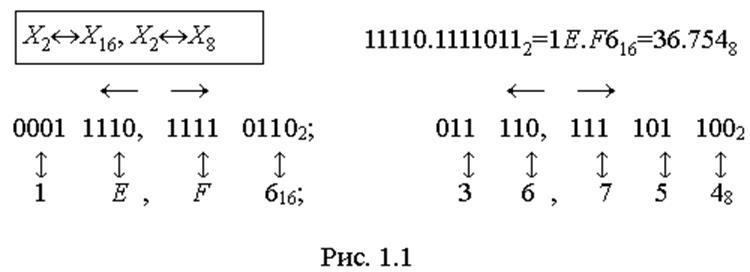
Взагалі, якщо основи двох систем співвідносяться як c2=c1k (k – ціле число), то для перетворення Xc1®Xc2 (чисел від системи з основою c1 до сис­теми з основою c2) досить розбити вихідне число Xc1 на групи з k цифр відносно коми та замінити кожну групу на цифру системи з основою c2. Так, для перетворень X2®X16,  X2®X8 (приклади на рис. 1.1) двійкове число роз­биваємо відносно коми ліворуч та праворуч (зазначено стрілками вгорі) відповідно по чотири (тетради) і три (тріади) розряди, додаємо в крайніх гру­пах, за необхідністю, незначущі нулі та замінюємо утворені тетради й тріади цифрами відпо-відно шістнадцяткової і вісімкової СЧ. І, навпаки, для зворот­ного перетворення X16®X2, X8®X2 кожну цифру числа замінюємо відповідно тетрадою або тріадою двійкових цифр.

1.1.3. Перетворення до десяткової системи числення

Часто доводиться перетворювати числа з будь-якої СЧ до звичної десят­кової системи. Універсальним для цього є метод за формулою полінома (1.2). Для СЧ із великими основами, наприклад, c=16 (рис. 1.2,а), можна скориста­тися таблицями степенів та мікрокалькулятором, а для двійкової системи до­сить підсумувати вагові коефіцієнти (на рис. 1.2,б розташовані  вгорі), що відповідають одиничним розрядам двійкового числа.

Якщо у виразі (1.2) поступово виносити за дужки основу в першому степені, одержимо модифіковану формулу, в якій менше операцій множення та яку легше запрограмувати. Обчислення за нею (алгоритм Горнера) розглянемо на прикладі (рис. 1.2,в). Старший розряд числа (B) множимо на основу системи (c=16), до добутку додаємо наступний розряд (A) і суму (186) знов множимо на основу; продовжуючи цей ланцюжок, під кінець до попереднього обутку додаємо останній розряд (0) цілої частини вихідного числа й дістаємо, таким чином, цілу частину десяткового числа (2976). Перетворення дробової частини виконується аналогічно, але в протилежному напрямку. Молодший розряд дробової частини (F) ділимо на основу системи (або множимо на 1/c=0,0625), до результату додаємо наступний ліворуч розряд (8) і суму (8,9375) знов ділимо на основу. Після додавання останнього (першого після коми) розряду (0) також виконуємо ділення і дістаємо дробову частину числа (0,0349...). У підсумку маємо BA0,08F16 »2976,034910.

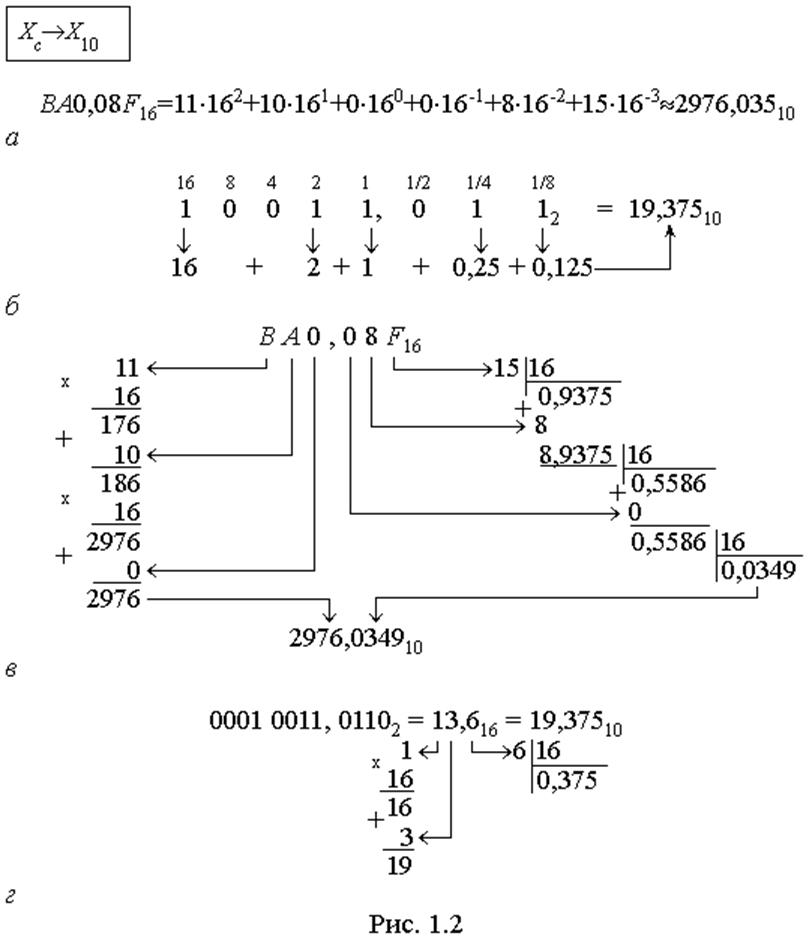
Перетворення до десяткової СЧ за алгоритмом Горнера можна робити і з двійкової системи, проте для довгих чисел воно коротше за схемою X2 ® X16 ® X10 (рис. 1.2,г).

1.1.4. Перетворення від десяткової до інших систем числення

Для зображення чисел і іншої інформації в цифрових пристроях часто необхідно перетворювати десяткові числа до СЧ з будь-якою основою c. Універсальний алгоритм такого перетворення розглянемо на прикладі Х10 ® ®Х16 (рис. 1.3,а).

Цілу частину вихідного числа (2976) і кожну наступну частку (186) ділять послідовно на основу нової системи (c=16) до отримання неподільної частки (11). Записуючи останню частку (11) і залишки від ділення (10; 0) як цифри нової  системи (B;  A; 0)  у  зворотному  порядку  їх  здобуття,  дістають  цілу

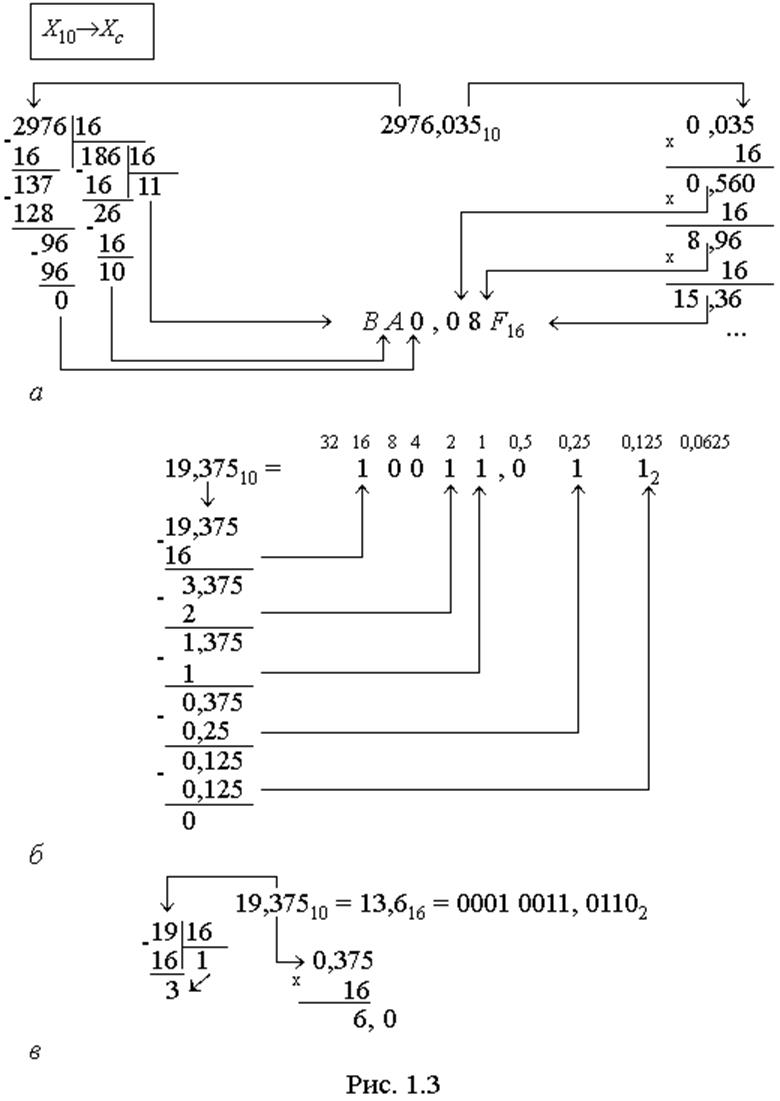
частину нового числа (BA016). Дробову частину вихідного числа (0,035) і дробову частину кожного наступного добутку (0,56; 0,96; ...) тепер множать послідовно на ту ж саму основу (16) до отримання нуля в дробовій частині чергового добутку або потрібної точності (кількості розрядів після коми). Цілі частини добутків від кожного множення (0; 8; 15; ...), записані як цифри нової СЧ (0; 8; F) у прямому порядку їх одержання, складають дробову  частину нового числа (0,08F...16). Таким чином, маємо 2976,03510 »BA0,08F16.